บ้าน-กระต่าย-1 9 รูท 3 กำลังของ 2 วิธีคำนวณรากที่สามที่ง่ายและไม่ง่ายนัก

1 9 รูท 3 กำลังของ 2 วิธีคำนวณรากที่สามที่ง่ายและไม่ง่ายนัก

ขอแสดงความยินดี: วันนี้เราจะดูที่ราก - หนึ่งในหัวข้อที่น่าเหลือเชื่อที่สุดในชั้นประถมศึกษาปีที่ 8 :)

หลายคนสับสนเกี่ยวกับราก ไม่ใช่เพราะมันซับซ้อน (ซึ่งมีความซับซ้อนมากเกี่ยวกับมัน - คำจำกัดความสองสามข้อและคุณสมบัติอีกสองสามอย่าง) แต่เนื่องจากในตำราเรียนส่วนใหญ่รากถูกกำหนดผ่านป่าที่มีเพียงผู้เขียนหนังสือเรียนเท่านั้น ตนเองก็สามารถเข้าใจงานเขียนนี้ได้ และถึงอย่างนั้นก็มีเพียงวิสกี้ดีๆ สักขวด :)

ดังนั้นตอนนี้ฉันจะให้คำจำกัดความของรูทที่ถูกต้องและมีความสามารถมากที่สุด - สิ่งเดียวที่คุณควรจำจริงๆ จากนั้นฉันจะอธิบาย: เหตุใดจึงจำเป็นทั้งหมดนี้และจะนำไปใช้ในทางปฏิบัติได้อย่างไร

แต่ก่อนอื่นจำไว้อย่างหนึ่ง จุดสำคัญซึ่งคอมไพเลอร์ตำราเรียนหลายเล่มด้วยเหตุผลบางประการ "ลืม":

รากสามารถเป็นระดับคู่ได้ ($\sqrt(a)$ ที่เราชื่นชอบ เช่นเดียวกับ $\sqrt(a)$ ทุกประเภทและแม้แต่ $\sqrt(a)$) และดีกรีคี่ (ทุกประเภทของ $\sqrt (ก)$, $\ sqrt(ก)$ ฯลฯ) และคำจำกัดความของรากของดีกรีคี่นั้นค่อนข้างแตกต่างไปจากอันที่เป็นเลขคู่

อาจเป็นไปได้ว่า 95% ของข้อผิดพลาดและความเข้าใจผิดทั้งหมดที่เกี่ยวข้องกับรากเหง้าถูกซ่อนอยู่ใน "ค่อนข้างแตกต่าง" นี้ ดังนั้นเรามาทำความเข้าใจคำศัพท์กันให้ชัดเจน:

คำนิยาม. แม้กระทั่งราก nจากจำนวน $a$ เป็นจำนวนเท่าใดก็ได้ ไม่เป็นลบตัวเลข $b$ เป็นเช่นนั้น $((b)^(n))=a$ และรากที่เป็นคี่ของตัวเลขเดียวกัน $a$ โดยทั่วไปจะเป็นตัวเลข $b$ ใดๆ ที่มีความเท่าเทียมกันเท่ากัน: $((b)^(n))=a$

ไม่ว่าในกรณีใด รูทจะแสดงดังนี้:

\(ก)\]

จำนวน $n$ ในสัญลักษณ์ดังกล่าวเรียกว่าเลขชี้กำลังราก และจำนวน $a$ เรียกว่านิพจน์ราก โดยเฉพาะอย่างยิ่ง สำหรับ $n=2$ เราจะได้รากที่สอง "ที่ชื่นชอบ" ของเรา (ยังไงก็ตาม นี่คือรากของดีกรีคู่) และสำหรับ $n=3$ เราจะได้รากที่สาม (ดีกรีคี่) ซึ่งก็คือ มักพบในปัญหาและสมการด้วย

ตัวอย่าง. ตัวอย่างคลาสสิกรากที่สอง:

\[\begin(align) & \sqrt(4)=2; \\ & \sqrt(81)=9; \\ & \sqrt(256)=16. \\ \end(จัดแนว)\]

อย่างไรก็ตาม $\sqrt(0)=0$ และ $\sqrt(1)=1$ ซึ่งค่อนข้างสมเหตุสมผล เนื่องจาก $((0)^(2))=0$ และ $((1)^(2))=1$

รากของคิวบ์ก็เป็นเรื่องธรรมดาเช่นกัน - ไม่จำเป็นต้องกลัวมัน:

\[\begin(align) & \sqrt(27)=3; \\ & \sqrt(-64)=-4; \\ & \sqrt(343)=7. \\ \end(จัดแนว)\]

“ตัวอย่างที่แปลกใหม่” สองสามอย่าง:

\[\begin(align) & \sqrt(81)=3; \\ & \sqrt(-32)=-2. \\ \end(จัดแนว)\]

หากคุณไม่เข้าใจความแตกต่างระหว่างระดับคู่และระดับคี่ ให้อ่านคำจำกัดความอีกครั้ง มันสำคัญมาก!

ในระหว่างนี้ เราจะพิจารณาคุณลักษณะหนึ่งที่ไม่พึงประสงค์ของราก เนื่องจากเราจำเป็นต้องแนะนำคำจำกัดความที่แยกจากกันสำหรับเลขชี้กำลังคู่และเลขคี่

เหตุใดจึงจำเป็นต้องมีราก?

หลังจากอ่านคำจำกัดความแล้ว นักเรียนหลายคนจะถามว่า “นักคณิตศาสตร์สูบบุหรี่อะไรเมื่อพวกเขาคิดเรื่องนี้ขึ้นมา” และจริงๆ แล้ว: เหตุใดจึงจำเป็นต้องมีรากเหล่านี้ทั้งหมด?

เพื่อตอบคำถามนี้ เรามาย้อนกลับไปโรงเรียนประถมกันดีกว่า ข้อควรจำ: ในสมัยที่ห่างไกล เมื่อต้นไม้เขียวขจีและเกี๊ยวอร่อยมากขึ้น ความกังวลหลักของเราคือการคูณตัวเลขให้ถูกต้อง ก็ประมาณ "ห้าคูณห้า - ยี่สิบห้า" แค่นั้นเอง แต่คุณสามารถคูณตัวเลขได้ไม่ใช่เป็นคู่ แต่คูณเป็นแฝด สี่เท่า และโดยทั่วไปคือทั้งเซต:

\[\begin(align) & 5\cdot 5=25; \\ & 5\cdot 5\cdot 5=125; \\ & 5\cdot 5\cdot 5\cdot 5=625; \\ & 5\cdot 5\cdot 5\cdot 5\cdot 5=3125; \\ & 5\cdot 5\cdot 5\cdot 5\cdot 5\cdot 5=15\ 625. \end(จัดแนว)\]

อย่างไรก็ตามนี่ไม่ใช่ประเด็น เคล็ดลับนั้นแตกต่างออกไป นักคณิตศาสตร์เป็นคนเกียจคร้าน ดังนั้นพวกเขาจึงเป็นเรื่องยากลำบากในการเขียนการคูณสิบห้าดังนี้:

นั่นเป็นเหตุผลที่พวกเขาได้รับปริญญา ทำไมไม่เขียนจำนวนปัจจัยเป็นตัวยกแทนสตริงยาวล่ะ บางสิ่งเช่นนี้:

สะดวกมาก! การคำนวณทั้งหมดลดลงอย่างมาก และคุณไม่จำเป็นต้องเปลืองแผ่นหนังและสมุดโน้ตจำนวนมากเพื่อเขียนลงไปถึง 5,183 แผ่น บันทึกนี้เรียกว่ากำลังของจำนวน มีสมบัติมากมายอยู่ในนั้น แต่ความสุขกลับมีอายุสั้น

หลังจากงานเลี้ยงสังสรรค์สุดอลังการ ซึ่งจัดขึ้นเพื่อ "การค้นพบ" องศาเท่านั้น ทันใดนั้นนักคณิตศาสตร์หัวแข็งบางคนก็ถามขึ้นว่า "จะเป็นอย่างไรถ้าเรารู้ระดับของตัวเลขแต่ไม่ทราบตัวเลขนั้นเอง" ทีนี้ หากเรารู้ว่าจำนวน $b$ ยกกำลังที่ 5 ให้ 243 แล้วเราจะเดาได้อย่างไรว่าจำนวน $b$ นั้นเท่ากับเท่าใด

ปัญหานี้กลายเป็นปัญหาระดับโลกมากกว่าที่เห็นในครั้งแรก เพราะปรากฎว่าสำหรับพาวเวอร์ "สำเร็จรูป" ส่วนใหญ่ไม่มีตัวเลข "เริ่มต้น" ดังกล่าว ตัดสินด้วยตัวคุณเอง:

\[\begin(align) & ((b)^(3))=27\ลูกศรขวา b=3\cdot 3\cdot 3\ลูกศรขวา b=3; \\ & ((b)^(3))=64\ลูกศรขวา b=4\cdot 4\cdot 4\ลูกศรขวา b=4 \\ \end(จัดแนว)\]

จะเกิดอะไรขึ้นถ้า $((b)^(3))=50$? ปรากฎว่าเราต้องหาจำนวนจำนวนหนึ่งซึ่งเมื่อคูณด้วยตัวมันเอง 3 ครั้ง ก็จะได้ 50 แต่จำนวนนี้คืออะไร? มันมากกว่า 3 อย่างชัดเจน เนื่องจาก 3 3 = 27< 50. С тем же успехом оно меньше 4, поскольку 4 3 = 64 >50. นั่นคือ ตัวเลขนี้อยู่ระหว่างสามถึงสี่ แต่คุณจะไม่เข้าใจว่ามันเท่ากับอะไร

นี่คือเหตุผลว่าทำไมนักคณิตศาสตร์ถึงมีรากที่ $n$th นี่เป็นเหตุผลว่าทำไมจึงมีการใช้สัญลักษณ์ราก $\sqrt(*)$ เพื่อกำหนดจำนวน $b$ ซึ่งในระดับที่ระบุจะทำให้เราทราบค่าที่ทราบก่อนหน้านี้

\[\sqrt[n](a)=b\ลูกศรขวา ((b)^(n))=a\]

ฉันไม่เถียง: บ่อยครั้งที่รากเหล่านี้คำนวณได้ง่าย - เราเห็นตัวอย่างหลายประการข้างต้น แต่ในกรณีส่วนใหญ่ หากคุณนึกถึงตัวเลขใดๆ ก็ตามแล้วพยายามแยกรากของระดับใดๆ ออกมา คุณจะต้องเจอกับความเลวร้ายอย่างยิ่ง

มีอะไรอยู่! แม้แต่ $\sqrt(2)$ ที่ง่ายที่สุดและคุ้นเคยที่สุดก็ไม่สามารถแสดงในรูปแบบปกติของเราได้ - เป็นจำนวนเต็มหรือเศษส่วน และถ้าคุณใส่ตัวเลขนี้ลงในเครื่องคิดเลข คุณจะเห็นสิ่งนี้:

\[\sqrt(2)=1.414213562...\]

อย่างที่คุณเห็น หลังจากจุดทศนิยมจะมีลำดับตัวเลขที่ไม่สิ้นสุดซึ่งไม่เป็นไปตามตรรกะใดๆ แน่นอนว่าคุณสามารถปัดเศษตัวเลขนี้เพื่อเปรียบเทียบกับตัวเลขอื่นๆ ได้อย่างรวดเร็ว ตัวอย่างเช่น:

\[\sqrt(2)=1.4142...\ประมาณ 1.4 \lt 1.5\]

หรือนี่คืออีกตัวอย่างหนึ่ง:

\[\sqrt(3)=1.73205...\ประมาณ 1.7 \gt 1.5\]

แต่ประการแรกการปัดเศษทั้งหมดนี้ค่อนข้างหยาบ และประการที่สอง คุณต้องสามารถทำงานกับค่าโดยประมาณได้ ไม่เช่นนั้นคุณจะพบข้อผิดพลาดที่ไม่ชัดเจนมากมาย (โดยวิธีการ ทักษะในการเปรียบเทียบและการปัดเศษจะต้องได้รับการทดสอบในโปรไฟล์ Unified State Examination)

ดังนั้น ในทางคณิตศาสตร์แบบจริงจัง คุณไม่สามารถทำได้หากไม่มีราก - พวกมันเป็นตัวแทนที่เท่ากันของเซตของจำนวนจริงทั้งหมด $\mathbb(R)$ เช่นเดียวกับเศษส่วนและจำนวนเต็มที่เราคุ้นเคยมานานแล้ว

การไม่สามารถแสดงรากเป็นเศษส่วนของรูปแบบ $\frac(p)(q)$ หมายความว่ารากนี้ไม่ใช่ จำนวนตรรกยะ. ตัวเลขดังกล่าวเรียกว่าจำนวนอตรรกยะ และไม่สามารถแสดงได้อย่างแม่นยำ ยกเว้นด้วยความช่วยเหลือของโครงสร้างรากหรือการออกแบบอื่นๆ ที่ออกแบบมาโดยเฉพาะสำหรับสิ่งนี้ (ลอการิทึม ยกกำลัง ขีดจำกัด ฯลฯ) แต่เพิ่มเติมเกี่ยวกับเรื่องนี้อีกครั้ง

ลองพิจารณาหลายๆ ตัวอย่างที่หลังจากการคำนวณทั้งหมดแล้ว จำนวนอตรรกยะจะยังคงอยู่ในคำตอบ

\[\begin(align) & \sqrt(2+\sqrt(27))=\sqrt(2+3)=\sqrt(5)\ประมาณ 2.236... \\ & \sqrt(\sqrt(-32 ))=\sqrt(-2)\ประมาณ -1.2599... \\ \end(align)\]

ตามธรรมชาติแล้วตาม รูปร่างรูท แทบจะเป็นไปไม่ได้เลยที่จะเดาว่าตัวเลขใดจะอยู่หลังจุดทศนิยม อย่างไรก็ตาม คุณสามารถไว้วางใจในเครื่องคิดเลขได้ แต่แม้แต่เครื่องคำนวณวันที่ที่ทันสมัยที่สุดก็ยังให้แค่ตัวเลขสองสามหลักแรกของจำนวนอตรรกยะเท่านั้น ดังนั้นจึงถูกต้องกว่ามากถ้าเขียนคำตอบในรูปแบบ $\sqrt(5)$ และ $\sqrt(-2)$

นี่คือเหตุผลว่าทำไมพวกเขาถึงถูกประดิษฐ์ขึ้น เพื่อบันทึกคำตอบได้อย่างสะดวก

เหตุใดจึงต้องมีคำจำกัดความสองคำ?

ผู้อ่านที่สนใจอาจสังเกตเห็นแล้วว่ารากที่สองทั้งหมดที่ระบุในตัวอย่างนั้นนำมาจากจำนวนบวก อย่างน้อยก็ตั้งแต่เริ่มต้น แต่รากที่สามสามารถแยกออกจากจำนวนใดก็ได้อย่างใจเย็นไม่ว่าจะเป็นค่าบวกหรือค่าลบ

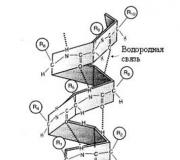
ทำไมสิ่งนี้ถึงเกิดขึ้น? ดูกราฟของฟังก์ชัน $y=((x)^(2))$:

กำหนดการ ฟังก์ชันกำลังสองให้รากสองประการ: บวกและลบ

ลองคำนวณ $\sqrt(4)$ โดยใช้กราฟนี้ เมื่อต้องการทำเช่นนี้ เส้นแนวนอน $y=4$ จะถูกวาดบนกราฟ (ทำเครื่องหมายด้วยสีแดง) ซึ่งตัดกับพาราโบลาที่จุดสองจุด: $((x)_(1))=2$ และ $((x )_(2)) =-2$. นี่ค่อนข้างสมเหตุสมผลเนื่องจาก

ทุกอย่างชัดเจนด้วยตัวเลขแรก - เป็นบวกดังนั้นจึงเป็นราก:

แต่แล้วจะทำอย่างไรกับประเด็นที่สอง? เหมือนสี่มีสองรากพร้อมกันเหรอ? ท้ายที่สุด ถ้าเรายกกำลังสองจำนวน −2 เราก็จะได้ 4 ด้วย ทำไมไม่เขียน $\sqrt(4)=-2$ ล่ะ? แล้วทำไมครูถึงมองกระทู้แบบนี้เหมือนอยากกินเธอ :)

ปัญหาคือถ้าคุณไม่กำหนดเงื่อนไขเพิ่มเติม รูปสี่เหลี่ยมจะมีรากที่สองสองตัว - บวกและลบ และจำนวนบวกใดๆ ก็จะมีสองตัวด้วย แต่จำนวนลบจะไม่มีรากเลย - เห็นได้จากกราฟเดียวกัน เนื่องจากพาราโบลาไม่เคยตกต่ำกว่าแกน ย, เช่น. ไม่ยอมรับค่าลบ

ปัญหาที่คล้ายกันนี้เกิดขึ้นกับรากทั้งหมดที่มีเลขชี้กำลังเป็นเลขคู่:

  1. พูดอย่างเคร่งครัด แต่ละจำนวนบวกจะมีรากสองตัวที่มีเลขชี้กำลังคู่ $n$;
  2. จากจำนวนลบ รากที่มีเลขคู่ $n$ จะไม่ถูกแยกออกมาเลย

นั่นคือสาเหตุว่าทำไมในคำจำกัดความรากของระดับเลขคู่ $n$ จึงกำหนดไว้โดยเฉพาะว่าคำตอบต้องเป็นจำนวนที่ไม่เป็นลบ นี่คือวิธีที่เรากำจัดความคลุมเครือ

แต่สำหรับ $n$ แปลก ๆ ก็ไม่มีปัญหาดังกล่าว หากต้องการดูสิ่งนี้ ลองดูกราฟของฟังก์ชัน $y=((x)^(3))$:

พาราโบลาลูกบาศก์สามารถรับค่าใดๆ ก็ได้ ดังนั้นรากที่สามจึงสามารถนำมาจากจำนวนใดก็ได้

จากกราฟนี้สามารถสรุปได้สองประการ:

  1. กิ่งก้านของลูกบาศก์พาราโบลานั้นแตกต่างจากแบบปกติตรงที่ไม่มีที่สิ้นสุดในทั้งสองทิศทาง - ทั้งขึ้นและลง ดังนั้นไม่ว่าเราจะวาดเส้นแนวนอนด้วยความสูงเท่าใด เส้นนี้จะตัดกับกราฟของเราอย่างแน่นอน ดังนั้น คิวบ์รูทจึงสามารถแยกออกจากจำนวนใดๆ ก็ได้เสมอ
  2. นอกจากนี้ จุดตัดดังกล่าวจะไม่ซ้ำกันเสมอ ดังนั้นคุณไม่จำเป็นต้องคิดว่าหมายเลขใดที่ถือว่าเป็นรากที่ "ถูกต้อง" และหมายเลขใดที่จะเพิกเฉย นั่นคือเหตุผลว่าทำไมการหารากของดีกรีคี่จึงง่ายกว่าการหาดีกรีคู่ (ไม่มีข้อกำหนดสำหรับการไม่ลบ)

น่าเสียดายที่เรื่องง่ายๆ เหล่านี้ไม่ได้อธิบายไว้ในหนังสือเรียนส่วนใหญ่ ในทางกลับกัน สมองของเราเริ่มทะยานขึ้นด้วยรากทางคณิตศาสตร์ทุกประเภทและคุณสมบัติของมัน

ใช่ ฉันไม่เถียง: คุณต้องรู้ด้วยว่ารูตเลขคณิตคืออะไร และฉันจะพูดถึงเรื่องนี้โดยละเอียดในบทเรียนแยกต่างหาก วันนี้เราจะมาพูดถึงเรื่องนี้ด้วย เพราะถ้าไม่มีความคิดทั้งหมดเกี่ยวกับรากของการคูณ $n$-th ก็จะไม่สมบูรณ์

แต่ก่อนอื่นคุณต้องเข้าใจคำจำกัดความที่ฉันให้ไว้ข้างต้นให้ชัดเจน มิฉะนั้นเนื่องจากคำศัพท์มากมาย ความยุ่งเหยิงดังกล่าวจะเริ่มต้นขึ้นในหัวของคุณซึ่งสุดท้ายแล้วคุณจะไม่เข้าใจอะไรเลย

สิ่งที่คุณต้องทำคือเข้าใจความแตกต่างระหว่างตัวบ่งชี้คู่และคี่ ดังนั้น มารวบรวมทุกสิ่งที่คุณจำเป็นต้องรู้เกี่ยวกับรูทอีกครั้ง:

  1. รากของดีกรีคู่มีอยู่จากเท่านั้น จำนวนลบและตัวมันเองจะเป็นจำนวนที่ไม่เป็นลบเสมอ สำหรับจำนวนลบ รากดังกล่าวไม่ได้ถูกกำหนดไว้
  2. แต่รากของระดับคี่นั้นมาจากจำนวนใดๆ ก็ตามและตัวมันเองสามารถเป็นจำนวนใดๆ ก็ได้ สำหรับจำนวนบวกก็จะเป็นค่าบวก และสำหรับจำนวนลบ ดังที่ตัวหมวกบอกเป็นนัย ค่าจะเป็นค่าลบ

มันยากไหม? ไม่ มันไม่ใช่เรื่องยาก ก็เป็นที่ชัดเจน? ใช่ มันชัดเจนมาก! ตอนนี้เราจะมาฝึกการคำนวณกันสักหน่อย

คุณสมบัติพื้นฐานและข้อจำกัด

รากมีคุณสมบัติและข้อจำกัดแปลก ๆ มากมาย ซึ่งจะกล่าวถึงในบทเรียนแยกต่างหาก ดังนั้นตอนนี้เราจะพิจารณาเฉพาะ "เคล็ดลับ" ที่สำคัญที่สุดซึ่งใช้เฉพาะกับรูทที่มีดัชนีคู่เท่านั้น ลองเขียนคุณสมบัตินี้เป็นสูตร:

\[\sqrt(((x)^(2n)))=\ซ้าย| x\ขวา|\]

กล่าวอีกนัยหนึ่ง ถ้าเรายกจำนวนขึ้นเป็นกำลังคู่แล้วแยกรากของกำลังเดียวกัน เราจะไม่ได้จำนวนเดิม แต่เป็นโมดูลัสของมัน นี่เป็นทฤษฎีบทง่ายๆ ที่สามารถพิสูจน์ได้อย่างง่ายดาย (ก็เพียงพอที่จะพิจารณา $x$ ที่ไม่ใช่ค่าลบแยกกัน และแยกค่าลบออกจากกัน) ครูพูดถึงเรื่องนี้อยู่ตลอดเวลาและมีให้ในหนังสือเรียนของโรงเรียนทุกเล่ม แต่ทันทีที่ต้องแก้สมการไร้เหตุผล (เช่น สมการที่มีเครื่องหมายกรณฑ์) นักเรียนก็ลืมสูตรนี้ไปอย่างเป็นเอกฉันท์

เพื่อให้เข้าใจปัญหาโดยละเอียด เราจะลืมสูตรทั้งหมดสักครู่แล้วลองคำนวณตัวเลขสองตัวตรงๆ กัน:

\[\sqrt(((3)^(4)))=?\quad \sqrt(((\left(-3 \right))^(4)))=?\]

นี้เป็นอย่างมาก ตัวอย่างง่ายๆ. คนส่วนใหญ่จะแก้ตัวอย่างแรก แต่หลายๆ คนกลับติดอยู่กับตัวอย่างที่สอง หากต้องการแก้ไขเรื่องไร้สาระโดยไม่มีปัญหา ให้พิจารณาขั้นตอนต่อไปนี้เสมอ:

  1. ขั้นแรก ให้ยกจำนวนขึ้นเป็นยกกำลังที่สี่ มันเป็นเรื่องง่าย คุณจะได้รับหมายเลขใหม่ที่สามารถพบได้แม้ในตารางสูตรคูณ
  2. และตอนนี้จากหมายเลขใหม่นี้จำเป็นต้องแยกรูทที่สี่ออก เหล่านั้น. ไม่มี "การลดลง" ของรากและพลังเกิดขึ้น - สิ่งเหล่านี้เป็นการกระทำตามลำดับ

ลองดูที่นิพจน์แรก: $\sqrt(((3)^(4)))$. แน่นอนว่าคุณต้องคำนวณนิพจน์ใต้รูทก่อน:

\[((3)^(4))=3\cdot 3\cdot 3\cdot 3=81\]

จากนั้นเราก็แยกรากที่สี่ของหมายเลข 81:

ทีนี้ลองทำแบบเดียวกันกับนิพจน์ที่สองกัน ขั้นแรก เรายกเลข −3 ขึ้นเป็นกำลังที่สี่ ซึ่งต้องคูณด้วยตัวมันเอง 4 ครั้ง:

\[((\left(-3 \right))^(4))=\left(-3 \right)\cdot \left(-3 \right)\cdot \left(-3 \right)\cdot \ ซ้าย(-3 \ขวา)=81\]

เราได้เลขบวกเพราะว่า ทั้งหมดงานนี้มี minuses 4 ประการและพวกมันทั้งหมดจะหักล้างกัน (ท้ายที่สุดแล้วการลบสำหรับการลบจะให้การบวก) จากนั้นเราก็แยกรากอีกครั้ง:

โดยหลักการแล้ว ไม่สามารถเขียนบรรทัดนี้ได้ เนื่องจากไม่ใช่เกมง่ายๆ ที่คำตอบจะเหมือนกัน เหล่านั้น. รากคู่ของพลังเท่ากัน "เผา" minuses และในแง่นี้ผลลัพธ์จึงแยกไม่ออกจากโมดูลปกติ:

\[\begin(align) & \sqrt(((3)^(4)))=\left| 3 \ขวา|=3; \\ & \sqrt(((\left(-3 \right))^(4)))=\left| -3 \ขวา|=3. \\ \end(จัดแนว)\]

การคำนวณเหล่านี้สอดคล้องกับคำนิยามรากของดีกรีคู่ โดยผลลัพธ์จะเป็นค่าที่ไม่เป็นลบเสมอ และเครื่องหมายกรณฑ์จะมีจำนวนที่ไม่เป็นลบเสมอ มิฉะนั้น รูทจะไม่ได้ถูกกำหนดไว้

หมายเหตุเกี่ยวกับขั้นตอน

  1. สัญกรณ์ $\sqrt(((a)^(2)))$ หมายความว่าเราต้องยกกำลังสองตัวเลข $a$ ก่อนแล้วจึงหารากที่สองของค่าผลลัพธ์ ดังนั้นเราจึงมั่นใจได้ว่าจะมีจำนวนที่ไม่เป็นลบอยู่ใต้เครื่องหมายรากเสมอ เนื่องจาก $((a)^(2))\ge 0$ ไม่ว่าในกรณีใดก็ตาม
  2. แต่ในทางกลับกัน สัญกรณ์ $((\left(\sqrt(a) \right))^(2))$ หมายความว่าเราหารากของจำนวน $a$ ก่อนแล้วจึงยกกำลังสองผลลัพธ์ ดังนั้นจำนวน $a$ จะเป็นค่าลบไม่ได้ไม่ว่าในกรณีใด นี่เป็นข้อกำหนดบังคับที่รวมอยู่ในคำจำกัดความ

ดังนั้นไม่ว่าในกรณีใดเราไม่ควรลดรากและองศาโดยไม่ได้ตั้งใจดังนั้นจึงถูกกล่าวหาว่า "ทำให้ง่ายขึ้น" การแสดงออกดั้งเดิม เพราะถ้ารากมีจำนวนลบและเลขชี้กำลังเป็นเลขคู่ เราจะพบปัญหามากมาย

อย่างไรก็ตาม ปัญหาทั้งหมดเหล่านี้เกี่ยวข้องกับตัวบ่งชี้คู่เท่านั้น

การลบเครื่องหมายลบออกจากใต้เครื่องหมายรูท

โดยธรรมชาติแล้ว รากที่มีเลขชี้กำลังคี่ก็มีลักษณะเฉพาะของตัวเองเช่นกัน ซึ่งโดยหลักการแล้วไม่มีอยู่ในเลขคู่ กล่าวคือ:

\[\sqrt(-a)=-\sqrt(a)\]

กล่าวโดยสรุป คุณสามารถลบเครื่องหมายลบออกจากใต้เครื่องหมายรากของดีกรีคี่ได้ นี้เป็นอย่างมาก ทรัพย์สินที่มีประโยชน์ซึ่งช่วยให้คุณ "โยน" เชิงลบทั้งหมดออกไป:

\[\begin(align) & \sqrt(-8)=-\sqrt(8)=-2; \\ & \sqrt(-27)\cdot \sqrt(-32)=-\sqrt(27)\cdot \left(-\sqrt(32) \right)= \\ & =\sqrt(27)\cdot \sqrt(32)= \\ & =3\cdot 2=6 \end(จัดแนว)\]

คุณสมบัติอย่างง่ายนี้ทำให้การคำนวณหลายอย่างง่ายขึ้นอย่างมาก ตอนนี้คุณไม่จำเป็นต้องกังวล: จะเกิดอะไรขึ้นถ้าการแสดงออกเชิงลบถูกซ่อนอยู่ใต้รูท แต่ระดับที่รูทกลับกลายเป็นเท่ากัน? มันก็เพียงพอแล้วที่จะ "โยน" minuses ทั้งหมดที่อยู่นอกรากออกไปหลังจากนั้นก็สามารถคูณซึ่งกันและกันแบ่งและทำสิ่งที่น่าสงสัยมากมายโดยทั่วไปซึ่งในกรณีของราก "คลาสสิก" รับประกันว่าจะนำเราไปสู่ ข้อผิดพลาด

และนี่คือคำจำกัดความอีกประการหนึ่งที่เข้ามาในฉาก - คำเดียวกับที่โรงเรียนส่วนใหญ่เริ่มศึกษาการแสดงออกที่ไม่มีเหตุผล และหากปราศจากเหตุผลของเราก็จะไม่สมบูรณ์ พบปะ!

รากเลขคณิต

สมมติสักครู่ว่าภายใต้เครื่องหมายรูทจะมีได้เฉพาะจำนวนบวกเท่านั้น หรือในกรณีที่รุนแรง อาจเป็นศูนย์ก็ได้ ลืมตัวบ่งชี้คู่/คี่ ลืมคำจำกัดความทั้งหมดที่ให้ไว้ข้างต้น เราจะใช้เฉพาะกับตัวเลขที่ไม่เป็นลบเท่านั้น แล้วไงล่ะ?

จากนั้นเราจะได้รากทางคณิตศาสตร์ซึ่งบางส่วนทับซ้อนกับคำจำกัดความ "มาตรฐาน" ของเรา แต่ก็ยังแตกต่างจากคำจำกัดความเหล่านั้น

คำนิยาม. รากเลขคณิตของระดับ $n$th ของจำนวนที่ไม่เป็นลบ $a$ คือจำนวนที่ไม่เป็นลบ $b$ โดยที่ $((b)^(n))=a$

ดังที่เราเห็น เราไม่สนใจเรื่องความเท่าเทียมอีกต่อไป กลับมีข้อจำกัดใหม่ปรากฏขึ้น: การแสดงออกที่รุนแรงตอนนี้ไม่เป็นลบเสมอ และรากเองก็ไม่เป็นลบเช่นกัน

เพื่อให้เข้าใจได้ดีขึ้นว่ารากเลขคณิตแตกต่างจากรากปกติอย่างไร ลองดูกราฟของสแควร์และพาราโบลาลูกบาศก์ที่เราคุ้นเคยอยู่แล้ว:

พื้นที่ค้นหารากเลขคณิต - ตัวเลขที่ไม่เป็นลบ

อย่างที่คุณเห็น จากนี้ไปเราจะสนใจเฉพาะกราฟที่อยู่ในไตรมาสพิกัดแรกเท่านั้น โดยที่พิกัด $x$ และ $y$ เป็นบวก (หรืออย่างน้อยเป็นศูนย์) คุณไม่จำเป็นต้องดูตัวบ่งชี้อีกต่อไปเพื่อทำความเข้าใจว่าเรามีสิทธิ์ใส่จำนวนลบไว้ใต้รากหรือไม่ เพราะจำนวนติดลบไม่ถือเป็นหลักการอีกต่อไป

คุณอาจถามว่า: “ทำไมเราจึงต้องมีคำจำกัดความที่ทำหมันเช่นนี้?” หรือ: “เหตุใดเราจึงใช้คำจำกัดความมาตรฐานที่ให้ไว้ข้างต้นไม่ได้”

ฉันจะให้คุณสมบัติเพียงรายการเดียวเนื่องจากคำจำกัดความใหม่มีความเหมาะสม ตัวอย่างเช่น กฎสำหรับการยกกำลัง:

\[\sqrt[n](a)=\sqrt(((a)^(k)))\]

โปรดทราบ: เราสามารถเพิ่มนิพจน์รากให้เป็นกำลังใดก็ได้และในเวลาเดียวกันก็คูณเลขชี้กำลังรูตด้วยกำลังเดียวกัน - และผลลัพธ์จะเป็นตัวเลขเดียวกัน! นี่คือตัวอย่าง:

\[\begin(align) & \sqrt(5)=\sqrt(((5)^(2)))=\sqrt(25) \\ & \sqrt(2)=\sqrt(((2)^ (4)))=\sqrt(16)\\ \end(align)\]

แล้วเรื่องใหญ่คืออะไร? ทำไมเราไม่ทำเช่นนี้มาก่อน? นี่คือเหตุผล ลองพิจารณานิพจน์ง่ายๆ: $\sqrt(-2)$ - จำนวนนี้ค่อนข้างปกติในความเข้าใจแบบคลาสสิกของเรา แต่ยอมรับไม่ได้อย่างแน่นอนจากมุมมองของรากเลขคณิต ลองแปลงมันดู:

$\begin(align) & \sqrt(-2)=-\sqrt(2)=-\sqrt(((2)^(2)))=-\sqrt(4) \lt 0; \\ & \sqrt(-2)=\sqrt(((\left(-2 \right))^(2)))=\sqrt(4) \gt 0. \\ \end(align)$

อย่างที่คุณเห็น ในกรณีแรกเราลบเครื่องหมายลบออกจากใต้ราก (เรามีสิทธิ์ทุกประการเนื่องจากเลขชี้กำลังเป็นเลขคี่) และในกรณีที่สองเราใช้สูตรด้านบน เหล่านั้น. จากมุมมองทางคณิตศาสตร์ ทุกอย่างเป็นไปตามกฎเกณฑ์

ว้าย! จำนวนเดียวกันจะเป็นทั้งบวกและลบได้อย่างไร? ไม่มีทาง. เพียงแต่ว่าสูตรสำหรับการยกกำลังซึ่งใช้ได้ผลดีกับจำนวนบวกและศูนย์นั้น เริ่มก่อให้เกิดความบาปโดยสมบูรณ์ในกรณีของจำนวนลบ

เพื่อที่จะกำจัดความคลุมเครือดังกล่าวจึงมีการคิดค้นรากทางคณิตศาสตร์ขึ้นมา มีบทเรียนใหญ่แยกต่างหากสำหรับพวกเขาโดยเราจะพิจารณาคุณสมบัติทั้งหมดอย่างละเอียด ดังนั้นเราจะไม่อยู่กับพวกเขาตอนนี้ - บทเรียนกลายเป็นเรื่องยาวเกินไปแล้ว

รากพีชคณิต: สำหรับผู้ที่ต้องการทราบข้อมูลเพิ่มเติม

ฉันคิดอยู่นานว่าจะแยกหัวข้อนี้ออกเป็นย่อหน้าแยกกันหรือไม่ ในที่สุดฉันก็ตัดสินใจทิ้งมันไว้ที่นี่ วัสดุนี้มีไว้สำหรับผู้ที่ต้องการเข้าใจรากเหง้าที่ดียิ่งขึ้น - ไม่ได้อยู่ในระดับ "โรงเรียน" โดยเฉลี่ยอีกต่อไป แต่อยู่ในระดับที่ใกล้เคียงกับระดับโอลิมปิก

ดังนั้น: นอกเหนือจากคำจำกัดความ "คลาสสิก" ของรากที่ $n$th ของตัวเลขและการหารที่เกี่ยวข้องกันเป็นเลขชี้กำลังคู่และคี่แล้ว ยังมีคำจำกัดความ "ผู้ใหญ่" อีกประเภทหนึ่งที่ไม่ได้ขึ้นอยู่กับความเท่าเทียมกันและรายละเอียดปลีกย่อยอื่น ๆ เลย สิ่งนี้เรียกว่ารากพีชคณิต

คำนิยาม. รากที่ $n$th เชิงพีชคณิตของ $a$ ใดๆ คือเซตของตัวเลข $b$ ทั้งหมด โดยที่ $((b)^(n))=a$ ไม่มีการกำหนดไว้สำหรับรากดังกล่าว ดังนั้นเราจะใส่เส้นประไว้ด้านบน:

\[\overline(\sqrt[n](a))=\left\( b\left| b\in \mathbb(R);((b)^(n))=a \right. \right\) \]

ความแตกต่างพื้นฐานจากคำจำกัดความมาตรฐานที่ให้ไว้ตอนต้นบทเรียนก็คือ รากพีชคณิตไม่ใช่จำนวนเฉพาะ แต่เป็นเซต และเนื่องจากเราทำงานกับจำนวนจริง ชุดนี้จึงมีเพียงสามประเภทเท่านั้น:

  1. ชุดเปล่า. เกิดขึ้นเมื่อคุณต้องการค้นหารากพีชคณิตของระดับคู่จากจำนวนลบ
  2. ชุดที่ประกอบด้วยองค์ประกอบเดียว รากทั้งหมดของเลขยกกำลังคี่ เช่นเดียวกับรากของเลขยกกำลังคู่ของศูนย์ อยู่ในหมวดหมู่นี้
  3. ในที่สุด เซตนี้สามารถมีตัวเลขสองตัวได้ - $((x)_(1))$ และ $((x)_(2))=-((x)_(1))$ เดียวกันกับที่เราเห็นบน ฟังก์ชันกำลังสองของกราฟ ดังนั้นการจัดเรียงดังกล่าวจึงเป็นไปได้เฉพาะเมื่อแยกรากของระดับเลขคู่ออกจากจำนวนบวกเท่านั้น

กรณีสุดท้ายสมควรได้รับการพิจารณาโดยละเอียดยิ่งขึ้น ลองนับตัวอย่างสักสองสามตัวอย่างเพื่อทำความเข้าใจความแตกต่าง

ตัวอย่าง. ประเมินนิพจน์:

\[\overline(\sqrt(4));\quad \overline(\sqrt(-27));\quad \overline(\sqrt(-16)).\]

สารละลาย. สำนวนแรกนั้นง่าย:

\[\overline(\sqrt(4))=\left\( 2;-2 \right\)\]

มันคือตัวเลขสองตัวที่เป็นส่วนหนึ่งของเซต เพราะแต่ละอันกำลังสองให้สี่

\[\overline(\sqrt(-27))=\left\( -3 \right\)\]

ตรงนี้เราเห็นชุดที่ประกอบด้วยตัวเลขเพียงตัวเดียว นี่เป็นตรรกะที่ค่อนข้างมาก เนื่องจากเลขชี้กำลังรูทเป็นเลขคี่

สุดท้ายนี้ สำนวนสุดท้าย:

\[\overline(\sqrt(-16))=\varnothing \]

เราได้รับชุดเปล่า เนื่องจากไม่มีจำนวนจริงสักตัวเดียวที่เมื่อยกกำลังสี่ (เช่น คู่!) จะทำให้เราได้จำนวนลบ −16

หมายเหตุสุดท้าย โปรดทราบ: ไม่ใช่เรื่องบังเอิญที่ฉันสังเกตเห็นทุกที่ที่เราทำงานกับจำนวนจริง เนื่องจากมีตัวเลขเชิงซ้อนด้วย จึงค่อนข้างเป็นไปได้ที่จะคำนวณ $\sqrt(-16)$ ตรงนั้น และอื่นๆ อีกมากมายที่แปลกประหลาด

อย่างไรก็ตามในยุคปัจจุบัน หลักสูตรของโรงเรียนในทางคณิตศาสตร์ จำนวนเชิงซ้อนแทบไม่เคยพบเลย พวกเขาถูกลบออกจากตำราเรียนส่วนใหญ่เนื่องจากเจ้าหน้าที่ของเราถือว่าหัวข้อนี้ "ยากเกินกว่าจะเข้าใจ"

เครื่องคิดเลขวิศวกรรมออนไลน์

เรากำลังรีบนำเสนอฟรีให้กับทุกคน เครื่องคิดเลขทางวิศวกรรม. ด้วยความช่วยเหลือ นักเรียนคนใดก็ตามสามารถทำการคำนวณทางคณิตศาสตร์ประเภทต่างๆ ทางออนไลน์ได้อย่างรวดเร็วและที่สำคัญที่สุด

เครื่องคิดเลขนำมาจากเว็บไซต์ - เครื่องคิดเลขวิทยาศาสตร์ web 2.0

เครื่องคิดเลขทางวิศวกรรมที่เรียบง่ายและใช้งานง่ายพร้อมอินเทอร์เฟซที่ไม่เกะกะและใช้งานง่ายจะเป็นประโยชน์ต่อผู้ใช้อินเทอร์เน็ตในวงกว้างอย่างแท้จริง ตอนนี้เมื่อใดก็ตามที่คุณต้องการเครื่องคิดเลข ให้ไปที่เว็บไซต์ของเราและใช้เครื่องคิดเลขทางวิศวกรรมฟรี

เครื่องคิดเลขทางวิศวกรรมสามารถทำได้ง่ายๆ การดำเนินการทางคณิตศาสตร์และการคำนวณทางคณิตศาสตร์ที่ค่อนข้างซับซ้อน

Web20calc เป็นเครื่องคิดเลขทางวิศวกรรมที่มีฟังก์ชันมากมาย เช่น วิธีคำนวณฟังก์ชันพื้นฐานทั้งหมด เครื่องคิดเลขยังรองรับ ฟังก์ชันตรีโกณมิติ, เมทริกซ์, ลอการิทึม และแม้แต่การลงจุด

ไม่ต้องสงสัยเลยว่า Web20calc จะเป็นที่สนใจของกลุ่มคนที่กำลังมองหา โซลูชั่นง่ายๆโทรเข้า เครื่องมือค้นหาคำขอ: คณิตศาสตร์ เครื่องคิดเลขออนไลน์. เว็บแอปพลิเคชันฟรีจะช่วยให้คุณคำนวณผลลัพธ์ของนิพจน์ทางคณิตศาสตร์บางอย่างได้ทันที เช่น ลบ บวก หาร แยกราก ยกกำลัง เป็นต้น

ในนิพจน์ คุณสามารถใช้การดำเนินการของการยกกำลัง การบวก การลบ การคูณ การหาร เปอร์เซ็นต์ และค่าคงที่ PI สำหรับการคำนวณที่ซับซ้อน ควรใส่วงเล็บไว้ด้วย

คุณสมบัติของเครื่องคิดเลขทางวิศวกรรม:

1. การดำเนินการทางคณิตศาสตร์ขั้นพื้นฐาน
2. การทำงานกับตัวเลขในรูปแบบมาตรฐาน
3. การคำนวณรากตรีโกณมิติ ฟังก์ชัน ลอการิทึม การยกกำลัง
4. การคำนวณทางสถิติ: การบวก ค่าเฉลี่ยเลขคณิต หรือส่วนเบี่ยงเบนมาตรฐาน
5. การใช้เซลล์หน่วยความจำและฟังก์ชันที่กำหนดเองของ 2 ตัวแปร
6. ทำงานกับมุมในรูปแบบเรเดียนและองศา

เครื่องคิดเลขทางวิศวกรรมช่วยให้สามารถใช้ฟังก์ชันทางคณิตศาสตร์ได้หลากหลาย:

การแยกราก (รากสี่เหลี่ยม ลูกบาศก์ และรากที่ n)
เช่น (e กำลัง x) เลขชี้กำลัง;
ฟังก์ชันตรีโกณมิติ: ไซน์ - บาป, โคไซน์ - คอส, แทนเจนต์ - แทน;
ฟังก์ชันตรีโกณมิติผกผัน: arcsine - sin-1, arccosine - cos-1, อาร์กแทนเจนต์ - tan-1;
ฟังก์ชันไฮเปอร์โบลิก: ไซน์ - ซินห์, โคไซน์ - cosh, แทนเจนต์ - tanh;
ลอการิทึม: ลอการิทึมไบนารีฐานสอง - log2x, ลอการิทึมฐานสิบ - บันทึก, ลอการิทึมธรรมชาติ - ln

เครื่องคิดเลขทางวิศวกรรมนี้ยังรวมถึงเครื่องคำนวณค่าที่สามารถแปลงได้ ปริมาณทางกายภาพสำหรับ ระบบต่างๆการวัด - หน่วยคอมพิวเตอร์ ระยะทาง น้ำหนัก เวลา ฯลฯ เมื่อใช้ฟังก์ชันนี้ คุณสามารถแปลงไมล์เป็นกิโลเมตร ปอนด์เป็นกิโลกรัม วินาทีเป็นชั่วโมง ฯลฯ ได้ทันที

หากต้องการคำนวณทางคณิตศาสตร์ ให้ป้อนลำดับก่อน นิพจน์ทางคณิตศาสตร์ในช่องที่เหมาะสม จากนั้นคลิกเครื่องหมายเท่ากับแล้วดูผลลัพธ์ คุณสามารถป้อนค่าได้โดยตรงจากแป้นพิมพ์ (สำหรับสิ่งนี้ พื้นที่เครื่องคิดเลขจะต้องทำงานอยู่ ดังนั้นจึงจะมีประโยชน์หากวางเคอร์เซอร์ในช่องป้อนข้อมูล) เหนือสิ่งอื่นใด คุณสามารถป้อนข้อมูลได้โดยใช้ปุ่มของเครื่องคิดเลขเอง

ในการสร้างกราฟ คุณควรเขียนฟังก์ชันในช่องป้อนข้อมูลตามที่ระบุไว้ในช่องพร้อมตัวอย่าง หรือใช้แถบเครื่องมือที่ออกแบบมาเป็นพิเศษสำหรับสิ่งนี้ (โดยคลิกที่ปุ่มที่มีไอคอนกราฟ) หากต้องการแปลงค่า ให้คลิกหน่วย หากต้องการทำงานกับเมทริกซ์ ให้คลิกเมทริกซ์

ถึงเวลาต้องจัดการมันแล้ว วิธีการสกัดราก. ขึ้นอยู่กับคุณสมบัติของราก โดยเฉพาะความเท่าเทียมกัน ซึ่งเป็นจริงสำหรับจำนวน b ใดๆ ที่ไม่ใช่ลบ

ด้านล่างเราจะดูวิธีการหลักในการแยกรากทีละรายการ

เริ่มจากกรณีที่ง่ายที่สุดกันก่อน - แยกรากออกจากจำนวนธรรมชาติโดยใช้ตารางสี่เหลี่ยม ตารางลูกบาศก์ ฯลฯ

ถ้าเป็นโต๊ะสี่เหลี่ยม ลูกบาศก์ ฯลฯ หากคุณไม่มีมัน ก็สมเหตุสมผลที่จะใช้วิธีการแยกราก ซึ่งเกี่ยวข้องกับการสลายจำนวนรากให้เป็นตัวประกอบเฉพาะ

เป็นเรื่องที่ควรค่าแก่การกล่าวถึงเป็นพิเศษถึงสิ่งที่เป็นไปได้สำหรับรากที่มีเลขชี้กำลังคี่

สุดท้ายนี้ ลองพิจารณาวิธีการที่ช่วยให้เราค้นหาตัวเลขของค่ารูทได้ตามลำดับ

มาเริ่มกันเลย.

การใช้โต๊ะสี่เหลี่ยม โต๊ะลูกบาศก์ ฯลฯ

ในส่วนใหญ่ กรณีง่ายๆตารางสี่เหลี่ยมลูกบาศก์ ฯลฯ ช่วยให้คุณสามารถแยกรากได้ ตารางเหล่านี้คืออะไร?

ตารางกำลังสองของจำนวนเต็มตั้งแต่ 0 ถึง 99 รวม (แสดงด้านล่าง) ประกอบด้วยสองโซน โซนแรกของตารางตั้งอยู่บนพื้นหลังสีเทา โดยการเลือกแถวที่ต้องการและคอลัมน์เฉพาะจะทำให้คุณสามารถเขียนตัวเลขตั้งแต่ 0 ถึง 99 ตัวอย่างเช่น ลองเลือกแถวที่มี 8 สิบและคอลัมน์ 3 หน่วย ซึ่งเราได้แก้ไขหมายเลข 83 แล้ว โซนที่สองครอบครองส่วนที่เหลือของตาราง แต่ละเซลล์จะอยู่ที่จุดตัดของแถวหนึ่งกับบางคอลัมน์ และมีช่องสี่เหลี่ยมของตัวเลขที่ตรงกันตั้งแต่ 0 ถึง 99 ที่จุดตัดของแถว 8 สิบและคอลัมน์ 3 ที่เราเลือกจะมีเซลล์ที่มีหมายเลข 6,889 ซึ่งเป็นกำลังสองของหมายเลข 83


ตารางลูกบาศก์ ตารางกำลังสี่ของตัวเลขตั้งแต่ 0 ถึง 99 และอื่นๆ คล้ายกับตารางสี่เหลี่ยม มีเพียงลูกบาศก์ กำลังสี่ ฯลฯ ในโซนที่สอง ตัวเลขที่สอดคล้องกัน

ตารางสี่เหลี่ยม ลูกบาศก์ กำลังสี่ ฯลฯ ช่วยให้คุณสามารถแยกรากที่สอง รากที่สาม รากที่สี่ ฯลฯ ตามลำดับจากตัวเลขในตารางเหล่านี้ ให้เราอธิบายหลักการใช้งานเมื่อทำการแยกราก

สมมติว่าเราจำเป็นต้องแยกรากที่ n ของตัวเลข a ในขณะที่ตัวเลข a อยู่ในตารางของกำลังที่ n เมื่อใช้ตารางนี้เราจะพบตัวเลข b โดยที่ a=b n แล้ว ดังนั้นเลข b จะเป็นรากที่ต้องการของดีกรีที่ n

ตามตัวอย่าง เราจะแสดงวิธีใช้ตารางคิวบ์เพื่อแยกรากที่สามของ 19,683 เราพบเลข 19,683 ในตารางลูกบาศก์ จากนั้นเราพบว่าเลขนี้คือเลขกำลังสามของเลข 27 ดังนั้น .


เห็นได้ชัดว่าตารางเลขยกกำลัง n สะดวกมากในการแยกราก อย่างไรก็ตาม สิ่งเหล่านี้มักจะไม่อยู่ในมือ และการคอมไพล์ต้องใช้เวลาพอสมควร ยิ่งไปกว่านั้น บ่อยครั้งจำเป็นต้องแยกรากออกจากตัวเลขที่ไม่อยู่ในตารางที่เกี่ยวข้อง ในกรณีเหล่านี้ คุณต้องหันไปใช้วิธีอื่นในการสกัดราก

แยกตัวประกอบจำนวนรากให้เป็นตัวประกอบเฉพาะ

เพียงพอ ด้วยวิธีที่สะดวกซึ่งทำให้สามารถแยกรากออกจากจำนวนธรรมชาติได้ (แน่นอนว่าถ้าแยกรากออก) ก็คือการสลายตัวของจำนวนรากให้เป็นตัวประกอบเฉพาะ ของเขา ประเด็นคือสิ่งนี้: หลังจากนั้นมันค่อนข้างง่ายที่จะแทนมันเป็นกำลังด้วยเลขชี้กำลังที่ต้องการซึ่งช่วยให้คุณได้รับค่าของรูท มาชี้แจงประเด็นนี้กัน

ให้รากที่ n ของจำนวนธรรมชาติ a มีค่าเท่ากับ b ในกรณีนี้ ความเท่าเทียมกัน a=b n เป็นจริง เบอร์ b เหมือนๆ กัน จำนวนธรรมชาติสามารถแสดงเป็นผลคูณของตัวประกอบเฉพาะทั้งหมด p 1 , p 2 , …, p m ในรูปแบบ p 1 · p 2 · … · p m และเลขราก a ในกรณีนี้แสดงเป็น (p 1 · p 2 · … · น.) น. เนื่องจากการสลายตัวของจำนวนหนึ่งไปเป็นตัวประกอบเฉพาะจะมีลักษณะเฉพาะ การสลายตัวของจำนวนราก a ไปเป็นตัวประกอบเฉพาะจะมีรูปแบบ (p 1 ·p 2 ·…·p m) n ซึ่งทำให้สามารถคำนวณค่าของรากได้ เช่น .

โปรดสังเกตว่าถ้าการสลายตัวไปเป็นตัวประกอบเฉพาะของจำนวนราก a ไม่สามารถแสดงในรูปแบบได้ (p 1 ·p 2 ·…·p m) n ดังนั้นรากที่ n ของจำนวน a จะยังไม่ถูกดึงออกจนหมด

ลองคิดดูเมื่อแก้ตัวอย่าง

ตัวอย่าง.

หารากที่สองของ 144

สารละลาย.

หากคุณดูตารางกำลังสองที่ให้ไว้ในย่อหน้าก่อนหน้า คุณจะเห็นได้ชัดเจนว่า 144 = 12 2 ซึ่งชัดเจนว่ารากที่สองของ 144 เท่ากับ 12

แต่เมื่อคำนึงถึงประเด็นนี้ เราสนใจว่ารากจะถูกแยกออกมาอย่างไรโดยการแยกเลขราก 144 ให้เป็นตัวประกอบเฉพาะ ลองดูวิธีแก้ปัญหานี้

มาย่อยสลายกันเถอะ 144 ถึงตัวประกอบเฉพาะ:

นั่นคือ 144=2·2·2·2·3·3 ขึ้นอยู่กับการสลายตัวที่เกิดขึ้น การเปลี่ยนแปลงต่อไปนี้สามารถดำเนินการได้: 144=2·2·2·2·3·3=(2·2) 2·3 2 =(2·2·3) 2 =12 2. เพราะฉะนั้น, .

การใช้คุณสมบัติของดีกรีและคุณสมบัติของราก อาจทำให้สูตรการแก้ปัญหาแตกต่างออกไปเล็กน้อย:

คำตอบ:

หากต้องการรวมวัสดุ ให้พิจารณาวิธีแก้ปัญหาของอีกสองตัวอย่าง

ตัวอย่าง.

คำนวณค่าของรูท

สารละลาย.

การแยกตัวประกอบเฉพาะของจำนวนราก 243 มีรูปแบบ 243=3 5 ดังนั้น, .

คำตอบ:

ตัวอย่าง.

ค่ารูตเป็นจำนวนเต็มหรือไม่?

สารละลาย.

เพื่อตอบคำถามนี้ ลองแยกจำนวนรากให้เป็นตัวประกอบเฉพาะแล้วดูว่าสามารถแสดงเป็นกำลังสามของจำนวนเต็มได้หรือไม่

เรามี 285 768=2 3 ·3 6 ·7 2. การขยายตัวที่เกิดขึ้นไม่สามารถแสดงเป็นกำลังสามของจำนวนเต็มได้ เนื่องจากกำลังของตัวประกอบเฉพาะ 7 ไม่ใช่ผลคูณของสาม ดังนั้น จึงไม่สามารถแยกรากที่สามของ 285,768 ได้อย่างสมบูรณ์

คำตอบ:

เลขที่

แยกรากออกจากเลขเศษส่วน

ถึงเวลาที่จะหาวิธีแยกรากออกมา จำนวนเศษส่วน. ให้เขียนเลขรากเศษส่วนเป็น p/q ตามคุณสมบัติของรากของผลหาร ความเท่าเทียมกันต่อไปนี้เป็นจริง จากความเท่าเทียมกันนี้เป็นไปตามนั้น กฎการแยกรากของเศษส่วน: รากของเศษส่วนเท่ากับผลหารของรากของตัวเศษหารด้วยรากของตัวส่วน

ลองดูตัวอย่างการแยกรากออกจากเศษส่วน

ตัวอย่าง.

สแควร์รูทของอะไร เศษส่วนทั่วไป 25/169 .

สารละลาย.

จากการใช้ตารางกำลังสอง เราพบว่ารากที่สองของตัวเศษของเศษส่วนเดิมเท่ากับ 5 และรากที่สองของตัวส่วนเท่ากับ 13 แล้ว . เป็นการเสร็จสิ้นการแยกรากของเศษส่วนร่วม 25/169

คำตอบ:

รากของเศษส่วนทศนิยมหรือจำนวนคละจะถูกแยกออกมาหลังจากแทนที่จำนวนรากด้วยเศษส่วนสามัญ

ตัวอย่าง.

หารากที่สามของเศษส่วนทศนิยม 474.552

สารละลาย.

ลองจินตนาการถึงเศษส่วนทศนิยมดั้งเดิมว่าเป็นเศษส่วนธรรมดา: 474.552=474552/1000 แล้ว . มันยังคงต้องแยกรากที่สามที่อยู่ในตัวเศษและตัวส่วนของเศษส่วนผลลัพธ์ เพราะ 474 552=2·2·2·3·3·3·13·13·13=(2 3 13) 3 =78 3 และ 1 000 = 10 3 จากนั้น และ . สิ่งที่เหลืออยู่คือการคำนวณให้เสร็จสิ้น .

คำตอบ:

.

การหารากของจำนวนลบ

คุ้มค่าที่จะจดจ่ออยู่กับการแยกรากออกจากจำนวนลบ เมื่อศึกษาราก เราบอกว่าเมื่อเลขชี้กำลังรากเป็นเลขคี่ ก็อาจมีเลขลบอยู่ใต้เครื่องหมายรากได้ เราให้ความหมายเหล่านี้แก่รายการเหล่านี้: สำหรับจำนวนลบ −a และเลขชี้กำลังคี่ของราก 2 n−1 . ความเท่าเทียมกันนี้ให้ กฎสำหรับการแยกรากคี่ออกจากจำนวนลบ: หากต้องการแยกรากของจำนวนลบ คุณต้องหารากของจำนวนบวกตรงข้าม และใส่เครื่องหมายลบไว้หน้าผลลัพธ์

ลองดูวิธีแก้ปัญหาตัวอย่าง

ตัวอย่าง.

ค้นหาค่าของราก

สารละลาย.

มาแปลงนิพจน์ดั้งเดิมเพื่อให้มีจำนวนบวกอยู่ใต้เครื่องหมายรูท: . ตอนนี้ หมายเลขผสมแทนที่ด้วยเศษส่วนธรรมดา: . เราใช้กฎในการแยกรากของเศษส่วนสามัญ: . ยังคงต้องคำนวณรากในตัวเศษและส่วนของเศษส่วนผลลัพธ์: .

นี่เป็นบทสรุปสั้นๆ ของวิธีแก้ปัญหา: .

คำตอบ:

.

การกำหนดค่ารูตในระดับบิต

ในกรณีทั่วไป ใต้รากจะมีตัวเลขจำนวนหนึ่งซึ่งไม่สามารถแสดงเป็นกำลังที่ n ของจำนวนใดๆ ได้ด้วยการใช้เทคนิคที่กล่าวถึงข้างต้น แต่ในขณะเดียวกันก็ต้องรู้ความหมายด้วย ให้รากอย่างน้อยก็ถึงสัญญาณที่แน่นอน ในกรณีนี้หากต้องการแยกรูทคุณสามารถใช้อัลกอริธึมที่ช่วยให้คุณได้รับค่าตัวเลขของตัวเลขที่ต้องการตามลำดับตามลำดับ

ขั้นตอนแรกของอัลกอริทึมนี้คือการค้นหาว่าบิตที่สำคัญที่สุดของค่ารูตคืออะไร ในการทำเช่นนี้ ตัวเลข 0, 10, 100, ... จะถูกยกกำลัง n ตามลำดับจนกระทั่งถึงช่วงเวลาที่ตัวเลขเกินจำนวนราก จากนั้นตัวเลขที่เรายกกำลัง n ในขั้นตอนก่อนหน้าจะระบุตัวเลขที่มีนัยสำคัญที่สุดที่สอดคล้องกัน

ตัวอย่างเช่น พิจารณาขั้นตอนนี้ของอัลกอริทึมเมื่อแยกข้อมูล รากที่สองจากห้า นำตัวเลข 0, 10, 100, ... มายกกำลังสองจนกระทั่งเราได้ตัวเลขที่มากกว่า 5 เรามี 0 2 = 0<5 , 10 2 =100>5 ซึ่งหมายความว่าหลักที่สำคัญที่สุดจะเป็นหลักหน่วย ค่าของบิตนี้และค่าที่ต่ำกว่าจะพบได้ในขั้นตอนถัดไปของอัลกอริธึมการแยกรูท

ขั้นตอนที่ตามมาทั้งหมดของอัลกอริธึมมีวัตถุประสงค์เพื่อชี้แจงค่าของรูทตามลำดับโดยการค้นหาค่าของบิตถัดไปของค่ารูทที่ต้องการโดยเริ่มจากค่าสูงสุดและเลื่อนไปที่ค่าต่ำสุด ตัวอย่างเช่น ค่าของรูตในขั้นตอนแรกกลายเป็น 2 ในขั้นตอนที่สอง – 2.2 ในขั้นตอนที่สาม – 2.23 และต่อ ๆ ไปใน 2.236067977… ให้เราอธิบายว่าจะหาค่าของตัวเลขได้อย่างไร

พบตัวเลขโดยการค้นหาผ่านค่าที่เป็นไปได้ 0, 1, 2, ..., 9 ในกรณีนี้ กำลังที่ n ของตัวเลขที่เกี่ยวข้องจะถูกคำนวณแบบขนาน และนำไปเปรียบเทียบกับจำนวนราก หากในบางขั้นตอนค่าของระดับเกินจำนวนรากจะถือว่าพบค่าของตัวเลขที่สอดคล้องกับค่าก่อนหน้าและจะทำการเปลี่ยนไปสู่ขั้นตอนถัดไปของอัลกอริธึมการแยกรูต หากสิ่งนี้ไม่เกิดขึ้น แล้วค่าของหลักนี้คือ 9

ให้เราอธิบายประเด็นเหล่านี้โดยใช้ตัวอย่างเดียวกันในการแยกรากที่สองของห้า

ก่อนอื่นเราจะหาค่าของหลักหน่วย เราจะผ่านค่า 0, 1, 2, ..., 9 โดยคำนวณ 0 2, 1 2, ..., 9 2 ตามลำดับจนกว่าเราจะได้ค่าที่มากกว่าเลขราก 5 สะดวกในการนำเสนอการคำนวณทั้งหมดเหล่านี้ในรูปแบบของตาราง:

ดังนั้นค่าของหลักหน่วยคือ 2 (เนื่องจาก 2 2<5 , а 2 3 >5) มาดูค่าของตำแหน่งในสิบกันดีกว่า. ในกรณีนี้เราจะยกกำลังสองตัวเลข 2.0, 2.1, 2.2, ..., 2.9 เปรียบเทียบค่าผลลัพธ์กับเลขราก 5:

ตั้งแต่ 2.2 2<5 , а 2,3 2 >5 แล้วค่าของตำแหน่งในสิบคือ 2 คุณสามารถดำเนินการค้นหาค่าของตำแหน่งที่ร้อยได้:

นี่คือวิธีที่หาค่าถัดไปของรากของห้าได้ ซึ่งก็คือ 2.23 ดังนั้นคุณจึงสามารถค้นหาค่าต่อไปได้: 2,236, 2,2360, 2,23606, 2,236067, … .

ในการรวมวัสดุเข้าด้วยกัน เราจะวิเคราะห์การแยกรากด้วยความแม่นยำระดับหนึ่งในร้อยโดยใช้อัลกอริธึมที่พิจารณา

ขั้นแรกเรากำหนดตัวเลขที่สำคัญที่สุด เมื่อต้องการทำเช่นนี้ เรายกกำลังสามของตัวเลข 0, 10, 100 ฯลฯ จนเราได้จำนวนที่มากกว่า 2,151,186 เรามี 0 3 = 0<2 151,186 , 10 3 =1 000<2151,186 , 100 3 =1 000 000>2 151,186 ดังนั้นเลขนัยสำคัญที่สุดคือหลักสิบ

มากำหนดมูลค่าของมันกัน

ตั้งแต่ 10 3<2 151,186 , а 20 3 >2 151.186 แล้วค่าหลักสิบคือ 1 มาดูหน่วยกันต่อ

ดังนั้น ค่าของหลักหน่วยคือ 2 เรามาต่อกันที่สิบกันดีกว่า

เนื่องจากแม้แต่ 12.9 3 ก็น้อยกว่าเลขราก 2 151.186 ดังนั้นค่าของตำแหน่งที่สิบคือ 9 ยังคงต้องดำเนินการขั้นตอนสุดท้ายของอัลกอริทึมโดยจะให้ค่าของรูทแก่เราด้วยความแม่นยำที่ต้องการ

ในขั้นตอนนี้ ค่าของรากจะพบว่าแม่นยำถึงหนึ่งในร้อย: .

โดยสรุปของบทความนี้ผมอยากจะบอกว่ามีวิธีอื่นอีกมากมายในการแยกราก แต่สำหรับงานส่วนใหญ่ งานที่เราศึกษาข้างต้นก็เพียงพอแล้ว

บรรณานุกรม.

  • Makarychev Yu.N., Mindyuk N.G., Neshkov K.I., Suvorova S.B. พีชคณิต: หนังสือเรียนสำหรับชั้นประถมศึกษาปีที่ 8 สถาบันการศึกษา.
  • โคลโมโกรอฟ เอ.เอ็น., อับรามอฟ เอ.เอ็ม., ดุดนิตซิน ยู.พี. และอื่น ๆ พีชคณิตและจุดเริ่มต้นของการวิเคราะห์: หนังสือเรียนสำหรับเกรด 10 - 11 ของสถาบันการศึกษาทั่วไป
  • Gusev V.A., Mordkovich A.G. คณิตศาสตร์ (คู่มือสำหรับผู้เข้าโรงเรียนเทคนิค)

คำแนะนำ

หากต้องการเพิ่มตัวเลขเป็น 1/3 ให้ป้อนตัวเลข จากนั้นคลิกปุ่มยกกำลัง และป้อนค่าประมาณ 1/3 - 0.333 ความแม่นยำนี้ค่อนข้างเพียงพอสำหรับการคำนวณส่วนใหญ่ อย่างไรก็ตาม ความแม่นยำของการคำนวณนั้นเพิ่มขึ้นได้ง่ายมาก - เพียงเพิ่มสามเท่าให้พอดีกับตัวบ่งชี้เครื่องคิดเลข (เช่น 0.3333333333333333) จากนั้นคลิกปุ่ม "="

หากต้องการคำนวณรูทที่สามโดยใช้คอมพิวเตอร์ ให้รันโปรแกรมเครื่องคิดเลข Windows ขั้นตอนการคำนวณรูตที่สามนั้นคล้ายกับที่อธิบายไว้ข้างต้นโดยสิ้นเชิง ข้อแตกต่างเพียงอย่างเดียวคือการออกแบบปุ่มยกกำลัง บนแป้นพิมพ์เสมือนของเครื่องคิดเลข จะแสดงเป็น "x^y"

รากที่สามสามารถคำนวณได้ใน MS Excel ในการดำเนินการนี้ ให้ป้อน “=” ในเซลล์ใดก็ได้แล้วเลือกไอคอน “insert” (fx) เลือกฟังก์ชัน "DEGREE" ในหน้าต่างที่ปรากฏขึ้นแล้วคลิกปุ่ม "OK" ในหน้าต่างที่ปรากฏขึ้น ให้ป้อนค่าของตัวเลขที่คุณต้องการคำนวณรากที่สาม ใน "ปริญญา" ให้ป้อนตัวเลข "1/3" พิมพ์ตัวเลข 1/3 ให้ตรงตามแบบฟอร์มนี้ - เหมือนเลขธรรมดา หลังจากนั้นคลิกปุ่ม "ตกลง" รากที่สามของตัวเลขที่กำหนดจะปรากฏในเซลล์ตารางที่ถูกสร้างขึ้น

หากต้องคำนวณรูตที่สามอย่างต่อเนื่อง ให้ปรับปรุงวิธีที่อธิบายไว้ข้างต้นเล็กน้อย สำหรับตัวเลขที่คุณต้องการแยกราก ให้ระบุไม่ใช่ตัวเลข แต่เป็นเซลล์ของตาราง หลังจากนั้นเพียงใส่หมายเลขเดิมลงในเซลล์นี้ทุกครั้ง - รากที่สามของมันจะปรากฏในเซลล์พร้อมกับสูตร

วิดีโอในหัวข้อ

บันทึก

บทสรุป. บทความนี้ตรวจสอบวิธีการต่างๆ ในการคำนวณค่ารากที่สาม ปรากฎว่าสามารถหาค่าของรูทคิวบ์ได้โดยใช้วิธีการวนซ้ำคุณยังสามารถประมาณรูทคิวบ์เพิ่มจำนวนเป็นกำลัง 1/3 ค้นหาค่าของรูทที่สามโดยใช้ Microsoft Office Ecxel การตั้งค่าสูตรในเซลล์

คำแนะนำที่เป็นประโยชน์

รากของดีกรีที่สองและสามมักใช้บ่อยเป็นพิเศษ ดังนั้นจึงมีชื่อพิเศษ รากที่สอง: ในกรณีนี้ โดยปกติแล้วเลขชี้กำลังจะถูกละไว้ และคำว่า "ราก" โดยไม่ระบุเลขชี้กำลังมักจะหมายถึงรากที่สอง การคำนวณอัลกอริธึมรากในทางปฏิบัติสำหรับการค้นหารากของระดับที่ n โดยปกติแล้วเครื่องคิดเลขทุกเครื่องจะมีรากที่สองและรากที่สามอยู่แล้ว

แหล่งที่มา:

  • รากที่สาม
  • วิธีหาค่ารากที่สองยกกำลัง N ใน Excel

การดำเนินการค้นหาราก ที่สาม องศามักเรียกว่าการแยกราก "ลูกบาศก์" และประกอบด้วยการค้นหาจำนวนจริงซึ่งลูกบาศก์จะให้ค่าเท่ากับจำนวนราก การดำเนินการแยกรากทางคณิตศาสตร์ใดๆ องศา n เท่ากับการดำเนินการยกกำลัง 1/n มีหลายวิธีที่คุณสามารถใช้เพื่อคำนวณรากที่สามได้

ถ้าคุณมีเครื่องคิดเลขอยู่แล้ว การแยกรากที่สามของตัวเลขใดๆ ก็ไม่มีปัญหาใดๆ แต่ถ้าคุณไม่มีเครื่องคิดเลขหรือแค่อยากทำให้คนอื่นประทับใจ ให้หารากที่สามด้วยมือ คนส่วนใหญ่จะพบว่ากระบวนการที่อธิบายไว้นี้ค่อนข้างซับซ้อน แต่ด้วยการฝึกฝน การแยกรากที่สามจะง่ายขึ้นมาก ก่อนที่คุณจะเริ่มอ่านบทความนี้ โปรดจำการคำนวณทางคณิตศาสตร์ขั้นพื้นฐานและการคำนวณด้วยตัวเลขกำลังสาม

ขั้นตอน

ส่วนที่ 1

การแยกรากที่สามโดยใช้ตัวอย่างง่ายๆ

    เขียนงาน.การเอารากที่สามด้วยมือก็คล้ายกับการหารยาวแต่มีความแตกต่างกันเล็กน้อย ขั้นแรก ให้เขียนงานในรูปแบบเฉพาะ

    • เขียนตัวเลขที่คุณต้องการหารากที่สาม แบ่งตัวเลขออกเป็นกลุ่มๆ ละสามหลัก โดยเริ่มจากจุดทศนิยม ตัวอย่างเช่น คุณต้องหารากที่สามของ 10 เขียนตัวเลขดังนี้: 10,000,000 จำนวนศูนย์เพิ่มเติมมีไว้เพื่อเพิ่มความแม่นยำของผลลัพธ์
    • วาดเครื่องหมายรากถัดจากและเหนือตัวเลข ให้คิดว่ามันเป็นเส้นแนวนอนและแนวตั้งที่คุณวาดเมื่อแบ่ง ข้อแตกต่างเพียงอย่างเดียวคือรูปร่างของป้ายทั้งสอง
    • วางจุดทศนิยมเหนือเส้นแนวนอน ทำเช่นนี้ให้อยู่เหนือจุดทศนิยมของตัวเลขเดิมโดยตรง

  1. จำผลลัพธ์ของจำนวนเต็มกำลังสามพวกเขาจะใช้ในการคำนวณ

    • 1 3 = 1 ∗ 1 ∗ 1 = 1 (\displaystyle 1^(3)=1*1*1=1)
    • 2 3 = 2 ∗ 2 ∗ 2 = 8 (\displaystyle 2^(3)=2*2*2=8)
    • 3 3 = 3 ∗ 3 ∗ 3 = 27 (\displaystyle 3^(3)=3*3*3=27)
    • 4 3 = 4 ∗ 4 ∗ 4 = 64 (\displaystyle 4^(3)=4*4*4=64)
    • 5 3 = 5 ∗ 5 ∗ 5 = 125 (\displaystyle 5^(3)=5*5*5=125)
    • 6 3 = 6 ∗ 6 ∗ 6 = 216 (\displaystyle 6^(3)=6*6*6=216)
    • 7 3 = 7 ∗ 7 ∗ 7 = 343 (\displaystyle 7^(3)=7*7*7=343)
    • 8 3 = 8 ∗ 8 ∗ 8 = 512 (\displaystyle 8^(3)=8*8*8=512)
    • 9 3 = 9 ∗ 9 ∗ 9 = 729 (\displaystyle 9^(3)=9*9*9=729)
    • 10 3 = 10 ∗ 10 ∗ 10 = 1,000 (\displaystyle 10^(3)=10*10*10=1000)

  2. ค้นหาตัวเลขตัวแรกของคำตอบเลือกลูกบาศก์ของจำนวนเต็มที่ใกล้เคียงที่สุดแต่เล็กกว่ากลุ่มแรกของตัวเลขสามหลัก

    • ในตัวอย่างของเรา กลุ่มแรกของตัวเลขสามหลักคือเลข 10 ค้นหาลูกบาศก์ที่ใหญ่ที่สุดที่น้อยกว่า 10 ลูกบาศก์นี้คือ 8 และรากที่สามของ 8 คือ 2
    • เหนือเส้นแนวนอนเหนือเลข 10 ให้เขียนเลข 2 จากนั้นจดค่าของการดำเนินการ 2 3 (\displaystyle 2^(3))= 8 ต่ำกว่า 10 ลากเส้นแล้วลบ 8 จาก 10 (เช่นเดียวกับการหารยาวปกติ) ผลลัพธ์คือ 2 (นี่คือเศษที่เหลือแรก)
    • ดังนั้นคุณจึงพบคำตอบหลักตัวแรกแล้ว พิจารณาว่าผลลัพธ์ที่ได้มีความแม่นยำเพียงพอหรือไม่ ในกรณีส่วนใหญ่ นี่จะเป็นคำตอบที่คร่าวๆ นำผลลัพธ์มายกกำลังสามเพื่อดูว่ามันใกล้กับตัวเลขเดิมแค่ไหน ในตัวอย่างของเรา: 2 3 (\displaystyle 2^(3))= 8 ซึ่งไม่ใกล้ 10 มากนัก จึงต้องคำนวณต่อไป

  3. ค้นหาหลักถัดไปของคำตอบเพิ่มกลุ่มที่สองซึ่งประกอบด้วยตัวเลขสามหลักเข้ากับเศษแรก และลากเส้นแนวตั้งทางด้านซ้ายของผลลัพธ์ ใช้ตัวเลขผลลัพธ์คุณจะพบหลักที่สองของคำตอบ ในตัวอย่างของเรา เราต้องเพิ่มกลุ่มที่สองซึ่งประกอบด้วยตัวเลขสามหลัก (000) เข้ากับเศษแรก (2) เพื่อให้ได้ตัวเลข 2000

    • ทางด้านซ้ายของเส้นแนวตั้ง คุณจะเขียนตัวเลขสามตัว ซึ่งผลรวมเท่ากับตัวประกอบแรกที่แน่นอน เว้นช่องว่างสำหรับตัวเลขเหล่านี้และใส่เครื่องหมายบวกระหว่างตัวเลขเหล่านั้น

  4. ค้นหาเทอมแรก (จากสาม)ในช่องว่างช่องแรก ให้เขียนผลลัพธ์ของการคูณตัวเลข 300 ด้วยกำลังสองของหลักแรกของคำตอบ (เขียนไว้เหนือเครื่องหมายราก) ในตัวอย่างของเรา ตัวเลขตัวแรกของคำตอบคือ 2 ดังนั้น 300*(2^2) = 300*4 = 1200 เขียน 1200 ในช่องว่างแรก เทอมแรกคือตัวเลข 1200 (บวกอีกสองตัวที่ต้องค้นหา)

    ค้นหาหลักที่สองของคำตอบหาคำตอบว่าต้องคูณ 1200 ด้วยจำนวนเท่าใดจึงจะได้ผลลัพธ์ใกล้เคียงกัน แต่ไม่เกิน 2000 จำนวนนี้ต้องเป็น 1 เท่านั้น เนื่องจาก 2 * 1200 = 2400 ซึ่งมากกว่า 2000 เขียน 1 (หลักที่สองของ คำตอบ) หลัง 2 และจุดทศนิยมเหนือเครื่องหมายรูท

    ค้นหาพจน์ที่สองและสาม (จากสาม)ตัวคูณประกอบด้วยตัวเลขสามตัว (เงื่อนไข) โดยตัวแรกที่คุณพบแล้ว (1200) ตอนนี้เราต้องค้นหาสองเทอมที่เหลือ

    • คูณ 3 ด้วย 10 และด้วยแต่ละหลักของคำตอบ (เขียนไว้เหนือเครื่องหมายรูท) ในตัวอย่างของเรา: 3*10*2*1 = 60 เพิ่มผลลัพธ์นี้เป็น 1200 และรับ 1260
    • สุดท้าย ให้ยกกำลังสองหลักสุดท้ายของคำตอบ ในตัวอย่างของเรา ตัวเลขหลักสุดท้ายของคำตอบคือ 1 ดังนั้น 1^2 = 1 ดังนั้น ตัวประกอบแรกจึงเท่ากับผลรวมของตัวเลขต่อไปนี้: 1200 + 60 + 1 = 1261 เขียนตัวเลขนี้ทางด้านซ้ายของ แถบแนวตั้ง

  5. คูณและลบ.คูณตัวเลขหลักสุดท้ายของคำตอบ (ในตัวอย่างของเราคือ 1) ด้วยตัวประกอบที่พบ (1261): 1*1261 = 1261 เขียนตัวเลขนี้ให้ต่ำกว่า 2000 แล้วลบออกจาก 2000 คุณจะได้ 739 (นี่คือเศษที่เหลือที่สอง ).

  6. พิจารณาว่าคำตอบที่คุณได้รับนั้นแม่นยำเพียงพอหรือไม่ทำเช่นนี้ทุกครั้งที่คุณลบออกอีกครั้ง หลังจากลบครั้งแรกแล้ว คำตอบคือ 2 ซึ่งไม่ใช่ผลลัพธ์ที่แน่ชัด หลังจากลบครั้งที่สองแล้ว คำตอบคือ 2.1

    • หากต้องการตรวจสอบความถูกต้องของคำตอบ ให้ยกกำลังสาม: 2.1*2.1*2.1 = 9.261
    • หากคุณคิดว่าคำตอบนั้นแม่นยำเพียงพอ คุณไม่จำเป็นต้องคำนวณต่อไป มิฉะนั้นให้ทำการลบอีกครั้ง

  7. ค้นหาปัจจัยที่สองหากต้องการฝึกการคำนวณและรับผลลัพธ์ที่แม่นยำยิ่งขึ้น ให้ทำซ้ำขั้นตอนข้างต้น

    • ในเศษที่สอง (739) ให้เพิ่มกลุ่มที่สามของตัวเลขสามหลัก (000) คุณจะได้หมายเลข 739000
    • คูณ 300 ด้วยกำลังสองของตัวเลขที่เขียนไว้เหนือเครื่องหมายราก (21): 300 ∗ 21 2 (\รูปแบบการแสดงผล 300*21^(2)) = 132300.
    • ค้นหาหลักที่สามของคำตอบ หาคำตอบว่าต้องคูณ 132300 ด้วยจำนวนเท่าใดจึงจะได้ผลลัพธ์ใกล้เคียงแต่ไม่เกิน 739000 จำนวนนี้คือ 5: 5 * 132200 = 661500 เขียน 5 (หลักที่สามของคำตอบ) หลัง 1 เหนือ เครื่องหมายราก
    • คูณ 3 ด้วย 10 ด้วย 21 และด้วยหลักสุดท้ายของคำตอบ (เขียนไว้เหนือเครื่องหมายรูท) ในตัวอย่างของเรา: 3 ∗ 21 ∗ 5 ∗ 10 = 3150 (\displaystyle 3*21*5*10=3150).
    • สุดท้าย ให้ยกกำลังสองหลักสุดท้ายของคำตอบ ในตัวอย่างของเรา ตัวเลขหลักสุดท้ายของคำตอบคือ 5 5 2 = 25. (\displaystyle 5^(2)=25.)
    • ดังนั้นตัวคูณที่สองคือ: 132300 + 3150 + 25 = 135475

  8. คูณตัวเลขหลักสุดท้ายของคำตอบด้วยตัวที่สองเมื่อคุณพบตัวประกอบตัวที่สองและตัวที่สามของคำตอบแล้ว ให้ดำเนินการดังนี้:

    • คูณตัวเลขสุดท้ายของคำตอบด้วยตัวประกอบที่พบ: 135475*5 = 677375
    • ลบ: 739000-677375 = 61625
    • พิจารณาว่าคำตอบที่คุณได้รับนั้นแม่นยำเพียงพอหรือไม่ เมื่อต้องการทำสิ่งนี้ ให้ยกกำลังสาม: 2 , 15 ∗ 2 , 15 ∗ 2 , 15 = 9 , 94 (\displaystyle 2.15*2.15*2.15=9.94).

  9. เขียนคำตอบของคุณผลลัพธ์ที่เขียนไว้เหนือเครื่องหมายราก คือคำตอบที่แม่นยำถึงทศนิยมสองตำแหน่ง ในตัวอย่างของเรา รากที่สามของ 10 คือ 2.15 ตรวจสอบคำตอบโดยยกกำลังสาม: 2.15^3 = 9.94 ซึ่งมีค่าประมาณ 10 หากคุณต้องการความแม่นยำมากกว่านี้ ให้คำนวณต่อ (ตามที่อธิบายไว้ข้างต้น)

    ส่วนที่ 2

    การแยกรากที่สามโดยใช้วิธีการประมาณค่า

    1. ใช้ลูกบาศก์ตัวเลขเพื่อกำหนดขีดจำกัดบนและล่างหากคุณต้องการหารากที่สามของจำนวนใดๆ ก็ตาม ให้หาลูกบาศก์ (ของตัวเลขบางตัว) ที่ใกล้กับตัวเลขที่กำหนด

      • ตัวอย่างเช่น คุณต้องหารากที่สามของ 600 เนื่องจาก 8 3 = 512 (\displaystyle 8^(3)=512)และ 9 3 = 729 (\displaystyle 9^(3)=729)ดังนั้นค่าของรากที่สามของ 600 จะอยู่ระหว่าง 8 ถึง 9 ดังนั้น ให้ใช้ตัวเลข 512 และ 729 เป็นขีดจำกัดบนและล่างของคำตอบ

    2. ประมาณการตัวเลขที่สองคุณพบเลขตัวแรกเนื่องจากความรู้เรื่องกำลังสามของจำนวนเต็ม ตอนนี้เปลี่ยนจำนวนเต็มให้เป็นเศษส่วนทศนิยมโดยเพิ่มตัวเลขจำนวนหนึ่งลงไป (หลังจุดทศนิยม) จาก 0 ถึง 9 คุณต้องค้นหาเศษส่วนทศนิยมที่มีลูกบาศก์อยู่ใกล้ แต่น้อยกว่าตัวเลขเดิม

      • ในตัวอย่างของเรา ตัวเลข 600 อยู่ระหว่างตัวเลข 512 ถึง 729 เช่น เพิ่มตัวเลข 5 เข้ากับตัวเลขแรกที่พบ (8) ตัวเลขที่คุณได้รับคือ 8.5
      • ในตัวอย่างของเรา: 8 , 5 ∗ 8 , 5 ∗ 8 , 5 = 614 , 1. (\displaystyle 8.5*8.5*8.5=614.1.)

    4. เปรียบเทียบกำลังสามของตัวเลขผลลัพธ์กับตัวเลขเดิม หากกำลังสามของตัวเลขผลลัพธ์มีขนาดใหญ่กว่าตัวเลขเดิม ให้ลองประมาณตัวเลขที่น้อยลง หากกำลังสามของตัวเลขผลลัพธ์มีขนาดเล็กกว่าตัวเลขเดิมมาก ให้ประเมินตัวเลขที่มากขึ้นจนกว่าลูกบาศก์ของหนึ่งในนั้นจะเกินจำนวนเดิม

      • ในตัวอย่างของเรา: 8 , 5 3 (\displaystyle 8.5^(3))> 600 ดังนั้นให้ประเมินจำนวนที่น้อยกว่าเป็น 8.4 นำตัวเลขนี้มายกกำลังสามแล้วเปรียบเทียบกับหมายเลขเดิม: 8 , 4 ∗ 8 , 4 ∗ 8 , 4 = 592 , 7 (\displaystyle 8.4*8.4*8.4=592.7). ผลลัพธ์นี้น้อยกว่าตัวเลขเดิม ดังนั้นรากที่สามของ 600 อยู่ระหว่าง 8.4 ถึง 8.5

    5. ประเมิน หมายเลขถัดไปเพื่อปรับปรุงความแม่นยำของคำตอบสำหรับแต่ละหมายเลขที่คุณประมาณไว้ล่าสุด ให้บวกตัวเลขตั้งแต่ 0 ถึง 9 จนกว่าคุณจะได้คำตอบที่แน่ชัด ในแต่ละรอบการประเมิน คุณจะต้องค้นหาขีดจำกัดบนและล่างระหว่างตัวเลขเดิม

      • ในตัวอย่างของเรา: 8 , 4 3 = 592 , 7 (\displaystyle 8.4^(3)=592.7)และ 8 , 5 3 = 614 , 1 (\displaystyle 8.5^(3)=614.1). ตัวเลขเดิม 600 ใกล้ 592 มากกว่า 614 ดังนั้น สำหรับตัวเลขสุดท้ายที่คุณประมาณไว้ ให้กำหนดตัวเลขที่ใกล้กับ 0 มากกว่า 9 ตัวอย่างเช่น ตัวเลขดังกล่าวคือ 4 ดังนั้น ให้ยกกำลังสามของตัวเลข 8.44

    6. หากจำเป็น ให้ประมาณตัวเลขอื่นเปรียบเทียบกำลังสามของตัวเลขผลลัพธ์กับตัวเลขเดิม หากกำลังสามของตัวเลขผลลัพธ์มีขนาดใหญ่กว่าตัวเลขเดิม ให้ลองประมาณตัวเลขที่น้อยลง กล่าวโดยสรุป คุณต้องหาตัวเลขสองตัวที่มีลูกบาศก์ใหญ่กว่าเล็กน้อยและเล็กกว่าตัวเลขเดิมเล็กน้อย

      • ในตัวอย่างของเรา 8 , 44 ∗ 8 , 44 ∗ 8 , 44 = 601 , 2 (\displaystyle 8.44*8.44*8.44=601.2). ซึ่งมากกว่าตัวเลขเดิมเล็กน้อย ดังนั้นให้ประมาณตัวเลขอื่น (น้อยกว่า) เช่น 8.43: 8 , 43 ∗ 8 , 43 ∗ 8 , 43 = 599 , 07 (\displaystyle 8.43*8.43*8.43=599.07). ดังนั้นรากที่สามของ 600 จึงอยู่ระหว่าง 8.43 ถึง 8.44

    7. ทำตามขั้นตอนที่อธิบายไว้จนกว่าคุณจะได้รับคำตอบที่คุณพอใจประมาณตัวเลขถัดไป เปรียบเทียบกับตัวเลขเดิม จากนั้นหากจำเป็น ให้ประมาณตัวเลขอื่น และอื่นๆ โปรดทราบว่าแต่ละหลักเพิ่มเติมหลังจุดทศนิยมจะเพิ่มความแม่นยำของคำตอบ

      • ในตัวอย่างของเรา ลูกบาศก์ 8.43 น้อยกว่าตัวเลขเดิมน้อยกว่า 1 หากคุณต้องการความแม่นยำมากกว่านี้ ให้ยกกำลัง 8.434 และรับ: 8, 434 3 = 599, 93 (\displaystyle 8,434^(3)=599,93)คือผลลัพธ์น้อยกว่าเลขเดิมน้อยกว่า 0.1


สิ่งพิมพ์ที่เกี่ยวข้อง: