Praca równa się sile w czasie. Praca mechaniczna i moc

Koń ciągnie wóz z pewną siłą, nazwijmy to F trakcja. Dziadek, siedząc na wózku, naciska na niego z pewną siłą. Oznaczmy to F ciśnienie Wózek porusza się w kierunku siły uciągu konia (w prawo), natomiast w kierunku siły nacisku dziadka (w dół) wóz się nie porusza. Dlatego w fizyce tak mówią F przyczepność działa na wózku i F ciśnienie nie działa na wózek.

Więc, działanie siły na ciało lub Praca mechaniczna– wielkość fizyczna, której moduł jest równy iloczynowi siły i drogi przebytej przez ciało wzdłuż kierunku działania tej siły S:

Na cześć angielskiego naukowca D. Joule'a nazwano jednostkę pracy mechanicznej 1 dżul(zgodnie ze wzorem 1 J = 1 N m).

Jeśli na dane ciało działa pewna siła, to działa na nie jakieś ciało. Dlatego działanie siły na ciało i działanie ciała na ciało to kompletne synonimy. Jednakże praca pierwszego ciała na drugim i praca drugiego ciała na pierwszym są częściowymi synonimami, ponieważ moduły tych prac są zawsze równe, a ich znaki są zawsze przeciwne. Dlatego we wzorze znajduje się znak „±”. Omówmy bardziej szczegółowo oznaki pracy.

Wartości liczbowe siły i ścieżki są zawsze wielkościami nieujemnymi. Natomiast praca mechaniczna może mieć zarówno znaki pozytywne, jak i negatywne. Jeżeli kierunek siły pokrywa się z kierunkiem ruchu ciała, to pracę wykonaną przez tę siłę uważa się za dodatnią. Jeżeli kierunek siły jest przeciwny do kierunku ruchu ciała, pracę wykonaną przez siłę uważa się za ujemną(bierzemy „–” ze wzoru „±”). Jeżeli kierunek ruchu ciała jest prostopadły do ​​kierunku działania siły, to taka siła nie wykonuje żadnej pracy, czyli A = 0.

Rozważmy trzy ilustracje przedstawiające trzy aspekty pracy mechanicznej.

Wykonywanie pracy na siłę może wyglądać inaczej z perspektywy różnych obserwatorów. Rozważmy przykład: dziewczyna jedzie windą. Czy wykonuje pracę mechaniczną? Dziewczyna może pracować tylko nad tymi ciałami, na które działa siła. Jest tylko jedno takie ciało - kabina windy, ponieważ dziewczyna swoim ciężarem naciska na podłogę. Teraz musimy się dowiedzieć, czy kabina jedzie w określonym kierunku. Rozważmy dwie opcje: z obserwatorem nieruchomym i ruchomym.

Niech najpierw chłopiec-obserwator usiądzie na ziemi. W związku z tym kabina windy porusza się w górę i pokonuje określoną odległość. Ciężar dziewczyny jest skierowany w przeciwnym kierunku - w dół, dlatego dziewczyna wykonuje negatywną pracę mechaniczną w kabinie: A rozw< 0. Вообразим, что мальчик-наблюдатель пересел внутрь кабины движущегося лифта. Как и ранее, вес девочки действует на пол кабины. Но теперь по отношению к такому наблюдателю кабина лифта не движется. Поэтому с точки зрения наблюдателя в кабине лифта девочка не совершает механическую работу: A deweloper = 0.

Pracę mechaniczną (pracę siły) znasz już z podstawowego kursu fizyki. Przypomnijmy podaną tam definicję pracy mechanicznej dla następujących przypadków.

Jeżeli siła jest skierowana w tym samym kierunku, co ruch ciała, to praca wykonana przez tę siłę

W tym przypadku praca wykonana przez siłę jest dodatnia.

Jeżeli siła jest skierowana przeciwnie do ruchu ciała, to jest to praca wykonana przez tę siłę

W tym przypadku praca wykonana przez siłę jest ujemna.

Jeżeli siła f_vec jest skierowana prostopadle do przemieszczenia s_vec ciała, to praca wykonana przez tę siłę wynosi zero:

Praca jest wielkością skalarną. Jednostka pracy nazywa się dżul (symbol: J) na cześć angielskiego naukowca Jamesa Joule’a, który grał ważna rola w odkryciu prawa zachowania energii. Ze wzoru (1) wynika:

1 J = 1 N * m.

1. Blok o masie 0,5 kg przesunięto po stole o 2 m, przykładając do niego siłę sprężystą 4 N (ryc. 28.1). Współczynnik tarcia między blokiem a stołem wynosi 0,2. Jaka jest praca działająca na blok?
a) grawitacja m?
b) normalne siły reakcji?
c) siły sprężyste?
d) siły tarcia ślizgowego tr?

Całkowitą pracę wykonaną przez kilka sił działających na ciało można obliczyć na dwa sposoby:
1. Znajdź pracę każdej siły i zsumuj te prace, biorąc pod uwagę znaki.
2. Znajdź wypadkową wszystkich sił przyłożonych do ciała i oblicz pracę wypadkowej.

Obie metody prowadzą do tego samego rezultatu. Aby się o tym przekonać, wróć do poprzedniego zadania i odpowiedz na pytania z zadania 2.

2. Co to jest równe:
a) suma pracy wykonanej przez wszystkie siły działające na klocek?
b) wypadkowa wszystkich sił działających na klocek?
c) wynik pracy? W ogólnym przypadku (kiedy siła f_vec jest skierowana pod dowolnym kątem do przemieszczenia s_vec) definicja pracy siły jest następująca.

Praca A stałej siły jest równa iloczynowi modułu siły F przez moduł przemieszczenia s i cosinus kąta α między kierunkiem siły a kierunkiem przemieszczenia:

A = Fs cos α (4)

3. Pokaż, że ogólna definicja pracy prowadzi do wniosków przedstawionych na poniższym schemacie. Sformułuj je ustnie i zapisz w zeszycie.

4. Do bloku znajdującego się na stole przykładana jest siła, której moduł wynosi 10 N. Dlaczego równy kątowi pomiędzy tą siłą a ruchem klocka, jeżeli przy przesuwaniu klocka po stole o 60 cm siła ta wykonała pracę: a) 3 J; b) –3 J; c) –3 J; D 6j? Wykonaj rysunki objaśniające.

2. Praca ciężkości

Niech ciało o masie m przesunie się pionowo od wysokości początkowej h n do wysokości końcowej h k.

Jeśli ciało porusza się w dół (h n > h k, ryc. 28.2, a), kierunek ruchu pokrywa się z kierunkiem grawitacji, dlatego praca grawitacji jest dodatnia. Jeśli ciało porusza się w górę (h n< h к, рис. 28.2, б), то работа силы тяжести отрицательна.

W obu przypadkach praca wykonana przez grawitację

A = mg(h n – h k). (5)

Obliczmy teraz pracę wykonaną przez grawitację podczas ruchu pod kątem do pionu.

5. Mały klocek o masie m ślizgał się po nachylonej płaszczyźnie o długości s i wysokości h (ryc. 28.3). Płaszczyzna nachylona tworzy kąt α z pionem.

a) Jaki jest kąt pomiędzy kierunkiem ciężkości a kierunkiem ruchu klocka? Zrób rysunek objaśniający.
b) Wyraź pracę grawitacji w m, g, s, α.
c) Wyraź s w kategoriach h i α.
d) Wyraź pracę grawitacji w m, g, h.
e) Jaka jest praca wykonana przez grawitację, gdy klocek porusza się w górę po całej płaszczyźnie?

Po wykonaniu tego zadania jesteś przekonany, że działanie grawitacji wyraża wzór (5) nawet wtedy, gdy ciało porusza się pod kątem do pionu - zarówno w dół, jak i w górę.

Ale wtedy wzór (5) na działanie grawitacji obowiązuje, gdy ciało porusza się po dowolnej trajektorii, ponieważ dowolną trajektorię (ryc. 28.4, a) można przedstawić jako zbiór małych „ pochyłe płaszczyzny„(ryc. 28.4, b).

Zatem,
pracę wykonaną przez grawitację podczas poruszania się po dowolnej trajektorii wyraża wzór

A t = mg(h n – h k),

gdzie h n jest początkową wysokością ciała, h k jest jego końcową wysokością.
Praca wykonana przez grawitację nie zależy od kształtu trajektorii.

Na przykład praca wykonana przez grawitację podczas przemieszczania ciała z punktu A do punktu B (ryc. 28.5) po trajektorii 1, 2 lub 3 jest taka sama. Stąd wynika w szczególności, że siła ciężkości podczas poruszania się po zamkniętej trajektorii (kiedy ciało powraca do punktu początkowego) jest równa zeru.

6. Kulkę o masie m zawieszoną na nitce o długości l odchylono o 90°, utrzymując nić napiętą, i puszczono bez pchania.
a) Jaka jest praca wykonana przez grawitację w czasie, w którym kula przemieszcza się do położenia równowagi (ryc. 28.6)?
b) Jaka jest praca wykonana przez siłę sprężystości nici w tym samym czasie?
c) Jaka jest praca wykonana przez wypadkowe siły przyłożone do piłki w tym samym czasie?

3. Praca siły sprężystej

Kiedy sprężyna powraca do stanu nieodkształconego, zawsze działa siła sprężystości pozytywna praca: jego kierunek pokrywa się z kierunkiem ruchu (ryc. 28.7).

Znajdźmy pracę wykonaną przez siłę sprężystości.
Moduł tej siły powiązany jest z modułem odkształcenia x zależnością (patrz § 15)

Pracę wykonaną przez taką siłę można zobaczyć graficznie.

Zauważmy najpierw, że praca wykonana przez stałą siłę jest liczbowo równa polu prostokąta pod wykresem siły w funkcji przemieszczenia (ryc. 28.8).

Rysunek 28.9 przedstawia wykres F(x) dla siły sprężystości. Podzielmy w myślach cały ruch ciała na tak małe odcinki, aby siłę działającą na każdy z nich można uznać za stałą.

Następnie praca na każdym z tych przedziałów jest liczbowo równa powierzchni figury pod odpowiednią sekcją wykresu. Cała praca jest równa sumie pracy w tych obszarach.

W związku z tym w tym przypadku praca jest liczbowo równa powierzchni figury pod wykresem zależności F(x).

7. Korzystając z rysunku 28.10, udowodnij to

pracę wykonaną przez siłę sprężystości po powrocie sprężyny do stanu nieodkształconego wyraża wzór

A = (kx 2)/2. (7)

8. Korzystając z wykresu na rysunku 28.11 udowodnij, że gdy odkształcenie sprężyny zmienia się od x n do x k, pracę siły sprężystości wyraża wzór

Ze wzoru (8) widzimy, że praca siły sprężystej zależy tylko od początkowego i końcowego odkształcenia sprężyny. Zatem jeśli ciało najpierw ulegnie odkształceniu, a następnie powróci do stanu początkowego, to praca siły sprężystej już tak zero. Przypomnijmy, że tę samą właściwość ma praca grawitacji.

9. W początkowej chwili napięcie sprężyny o sztywności 400 N/m wynosi 3 cm. Sprężyna jest rozciągnięta o kolejne 2 cm.
a) Jakie jest końcowe odkształcenie sprężyny?
b) Jaka jest praca wykonana przez siłę sprężystości sprężyny?

10. W początkowej chwili sprężyna o sztywności 200 N/m jest rozciągana o 2 cm, a w końcowej chwili ściskana o 1 cm. Jaka jest praca wykonana przez siłę sprężystości sprężyny?

4. Praca siły tarcia

Pozwól ciału przesuwać się po stałym wsporniku. Siła tarcia ślizgowego działająca na ciało jest zawsze skierowana przeciwnie do ruchu, dlatego praca siły tarcia ślizgowego jest ujemna w dowolnym kierunku ruchu (ryc. 28.12).

Dlatego jeśli przesuniemy klocek w prawo, a kołek o tę samą odległość w lewo, to mimo że powróci do pozycji wyjściowej, całkowita praca wykonana przez siłę tarcia ślizgowego nie będzie równa zeru. Jest to najważniejsza różnica pomiędzy pracą tarcia ślizgowego a pracą grawitacji i sprężystości. Przypomnijmy, że praca wykonana przez te siły podczas przemieszczania ciała po zamkniętej trajektorii wynosi zero.

11. Klocek o masie 1 kg przesuwano po stole tak, że jego tor był kwadratem o boku 50 cm.
a) Czy klocek powrócił do punktu początkowego?
b) Jaka jest całkowita praca wykonana przez siłę tarcia działającą na klocek? Współczynnik tarcia między blokiem a stołem wynosi 0,3.

5.Moc

Często ważny jest nie tylko rodzaj wykonywanej pracy, ale także szybkość, z jaką jest ona wykonywana. Charakteryzuje się mocą.

Moc P jest stosunkiem pracy wykonanej A do okresu czasu t, w którym praca ta została wykonana:

(Czasami moc w mechanice jest oznaczona literą N, a w elektrodynamice literą P. Uważamy, że wygodniej jest używać tego samego oznaczenia mocy.)

Jednostką mocy jest wat (symbol: W), nazwany na cześć angielskiego wynalazcy Jamesa Watta. Ze wzoru (9) wynika, że

1 W = 1 J/s.

12. Jaką moc rozwija człowiek podnosząc równomiernie wiadro z wodą o masie 10 kg na wysokość 1 m w ciągu 2 s?

Często wygodnie jest wyrazić moc nie poprzez pracę i czas, ale siłę i szybkość.

Rozważmy przypadek, gdy siła jest skierowana wzdłuż przemieszczenia. Wtedy praca wykonana przez siłę A = Fs. Podstawiając to wyrażenie do wzoru (9) na potęgę, otrzymujemy:

P = (Fs)/t = F(s/t) = Fv. (10)

13. Samochód jedzie po poziomej drodze z prędkością 72 km/h. Jednocześnie jego silnik rozwija moc 20 kW. Jaka jest siła oporu ruchu samochodu?

Wskazówka. Kiedy samochód porusza się po poziomej drodze ze stałą prędkością, siła uciągu jest równa sile oporu stawianego ruchowi samochodu.

14. Ile czasu zajmie równomierne wyrośnięcie? blok betonu o wadze 4 ton do wysokości 30 m, jeżeli moc silnika dźwigu wynosi 20 kW, a sprawność silnika elektrycznego dźwigu wynosi 75%?

Wskazówka. Sprawność silnika elektrycznego jest równa stosunkowi pracy podnoszenia ładunku do pracy silnika.

Dodatkowe pytania i zadania

15. Z balkonu o wysokości 10 i kącie 45° do poziomu wyrzucono piłkę o masie 200 g. Dotarcie w locie maksymalna wysokość 15 m piłka spadła na ziemię.
a) Jaka jest praca wykonana przez grawitację podczas podnoszenia piłki?
b) Jaka jest praca wykonana przez grawitację podczas opuszczania piłki?
c) Jaka jest praca wykonana przez grawitację podczas całego lotu piłki?
d) Czy w warunku znajdują się jakieś dodatkowe dane?

16. Kulka o masie 0,5 kg jest zawieszona na sprężynie o sztywności 250 N/m i znajduje się w równowadze. Kulka jest uniesiona w taki sposób, że sprężyna nie ulega odkształceniu i zostaje zwolniona bez pchnięcia.
a) Na jaką wysokość została podniesiona piłka?
b) Jaka jest praca wykonana przez grawitację w czasie, w którym kula przemieszcza się do położenia równowagi?
c) Jaka jest praca wykonana przez siłę sprężystości w czasie, w którym kula przemieszcza się do położenia równowagi?
d) Jaka jest praca wykonana przez wypadkową wszystkich sił przyłożonych do piłki w czasie, w którym piłka przemieszcza się do położenia równowagi?

17. Zjeżdżają z niego sanki o masie 10 kg zaśnieżona góra z kątem nachylenia α = 30° i przebyć określoną odległość powierzchnia pozioma(ryc. 28.13). Współczynnik tarcia sanek o śnieg wynosi 0,1. Długość podstawy góry wynosi l = 15 m.

a) Jaka jest wartość siły tarcia, gdy sanki poruszają się po poziomej powierzchni?
b) Jaka jest praca wykonana przez siłę tarcia, gdy sanki poruszają się po poziomej powierzchni na drodze 20 m?
c) Jaka jest wartość siły tarcia, gdy sanki poruszają się po górze?
d) Jaka jest praca wykonana przez siłę tarcia podczas opuszczania sań?
e) Jaka jest praca wykonana przez grawitację podczas opuszczania sań?
f) Jaka jest praca wykonana przez wypadkową siłę działającą na sanki schodzące z góry?

18. Samochód o masie 1 tony porusza się z prędkością 50 km/h. Silnik rozwija moc 10 kW. Zużycie benzyny wynosi 8 litrów na 100 km. Gęstość benzyny wynosi 750 kg/m 3 i jej ciepło właściwe spalanie 45 MJ/kg. Jaka jest wydajność silnika? Czy w warunku znajdują się jakieś dodatkowe dane?
Wskazówka. Sprawność silnika cieplnego jest równa stosunkowi pracy wykonanej przez silnik do ilości ciepła wydzielonego podczas spalania paliwa.

Charakterystyki energetyczne ruchu wprowadzane są w oparciu o koncepcję pracy mechanicznej lub pracy siły.

Praca A wykonana przez stałą siłę F → jest wielkością fizyczną równą iloczynowi modułów siły i przemieszczenia pomnożonego przez cosinus kąta α , znajdujący się pomiędzy wektorami siły F → i przemieszczeniem s →.

Ta definicja omówione na rysunku 1. 18 . 1.

Formuła pracy jest zapisana jako,

ZA = fa s cos α .

Praca jest wielkością skalarną. Dzięki temu możliwe jest uzyskanie wyniku dodatniego przy (0° ≤ α< 90 °) , отрицательной при (90 ° < α ≤ 180 °) . Когда задается прямой угол α , тогда совершаемая сила равняется нулю. Единицы измерения работы по системе СИ - джоули (Д ж) .

Dżul jest równy pracy wykonanej przez siłę 1 N podczas przemieszczania się o 1 m w kierunku działania tej siły.

Obrazek 1 . 18 . 1. Praca siły F →: A = F s cos α = F s s

Przy rzutowaniu F s → siły F → na kierunek ruchu s → siła nie pozostaje stała, a obliczenie pracy dla małych ruchów Δ s i sumuje się i oblicza według wzoru:

ZA = ∑ ∆ ZA ja = ∑ fa s ja ∆ s ja .

Ta ilość pracy jest obliczana z granicy (Δ s i → 0), a następnie przechodzi do całki.

Graficzną reprezentację dzieła określa się na podstawie obszaru krzywoliniowej figury znajdującej się pod wykresem F s (x) na rysunku 1. 18 . 2.

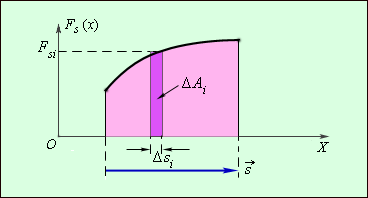
Obrazek 1 . 18 . 2. Graficzna definicja pracy Δ A i = F s ja Δ s ja .

Przykładem siły zależnej od współrzędnej jest siła sprężystości sprężyny, która jest zgodna z prawem Hooke'a. Aby rozciągnąć sprężynę, należy przyłożyć siłę F →, której moduł jest proporcjonalny do wydłużenia sprężyny. Można to zobaczyć na rysunku 1. 18 . 3.

Obrazek 1 . 18 . 3. Rozciągnięta wiosna. Kierunek siły zewnętrznej F → pokrywa się z kierunkiem ruchu s →. F s = k x, gdzie k oznacza sztywność sprężyny.

F → y p = - F →

Zależność modułu siły zewnętrznej od współrzędnych x można wykreślić linią prostą.

Obrazek 1 . 18 . 4. Zależność modułu siły zewnętrznej od współrzędnej przy rozciąganiu sprężyny.

Z powyższego rysunku można znaleźć pracę wykonaną nad siłą zewnętrzną prawego wolnego końca sprężyny, wykorzystując pole trójkąta. Formuła przyjmie formę

Wzór ten ma zastosowanie do wyrażenia pracy wykonanej przez siłę zewnętrzną podczas ściskania sprężyny. Obydwa przypadki pokazują, że siła sprężystości F → y p jest równa działaniu siły zewnętrznej F → , ale o przeciwnym znaku.

Definicja 2

Jeżeli na ciało działa kilka sił, wówczas wzór na pracę całkowitą będzie wyglądał jak suma całej pracy wykonanej na nim. Kiedy ciało porusza się translacyjnie, to znaczy, że punkty przyłożenia sił poruszają się równomiernie praca ogólna wszystkich sił będzie równa wypadkowej pracy przyłożonych sił.

Obrazek 1 . 18 . 5. Model pracy mechanicznej.

Określenie mocy

Moc nazywa się pracą wykonaną przez siłę w jednostce czasu.

Zapis wielkości fizycznej mocy, oznaczanej jako N, przyjmuje postać stosunku pracy A do czasu t wykonanej pracy, czyli:

Definicja 4

Układ SI wykorzystuje wat (W t) jako jednostkę mocy równą mocy siły, która wykonuje pracę 1 J w ciągu 1 s.

Jeśli zauważysz błąd w tekście, zaznacz go i naciśnij Ctrl+Enter

Energia- uniwersalny miernik różnych form ruchu i interakcji. Zmiana ruchu mechanicznego ciała jest spowodowana siły, działając na nią z innych ciał. Dzieła siły - proces wymiany energii pomiędzy oddziałującymi ze sobą ciałami.

Jeśli na ciele jest ruch prosty działa stała siła F, która tworzy pewien kąt  z kierunkiem ruchu, wówczas praca tej siły jest równa iloczynowi rzutu siły F S przez kierunek ruchu pomnożony przez przemieszczenie punktu przyłożenia siły: (1)

Ogólnie rzecz biorąc, siła może zmieniać się zarówno pod względem wielkości, jak i kierunku skalarny wartość np praca elementarna siły F przy przemieszczeniu dr:

gdzie  jest kątem między wektorami F i dr; ds = |dr| - ścieżka elementarna; F S - rzut wektora F na wektor dr Rys. 1

Praca siły na odcinku trajektorii od punktu 1 do momentu 2 równa sumie algebraicznej elementarnej pracy na poszczególnych nieskończenie małych odcinkach ścieżki: (2)

Gdzie S- przeszedł przez ciało. Kiedy </2 работа силы положительна, если >/2 praca wykonana przez tę siłę jest ujemna. Gdy =/2 (siła jest prostopadła do przemieszczenia), praca wykonana przez tę siłę wynosi zero.

Jednostka pracy - dżul(J): praca wykonana przez siłę 1 N na drodze 1 m (1 J = 1 N  m).

Moc– wartość prędkości pracy: (3)

W czasie d T siła F działa Fdr, a moc wytworzona przez tę siłę w danym momencie pasa: (4)

tj. jest równy iloczynowi skalarnemu wektora siły i wektora prędkości, z jaką porusza się punkt przyłożenia tej siły; N- ogrom skalarny.

Jednostka mocy - wat(W): moc, przy której praca 1J jest wykonywana w ciągu 1s (1W = 1J/s).

Energia kinetyczna i potencjalna

Energia kinetyczna układ mechaniczny - energia ruchu mechanicznego tego układu.

Siła F działająca na ciało pozostające w spoczynku i powodująca jego ruch, wykonuje pracę, a energia poruszającego się ciała zmienia się (d T) zwiększa się o ilość włożonej pracy, d A. Oznacza to, że dA = dT

Korzystając z drugiej zasady Newtona (F=mdV/dt) i szeregu innych transformacji otrzymujemy

(5) - energia kinetyczna ciała o masie m poruszającego się z prędkością w.

Energia kinetyczna zależy tylko od masy i prędkości ciała.

W różnych układy inercyjne odniesienia poruszające się względem siebie, prędkość ciała, a co za tym idzie jego energia kinetyczna, nie będą takie same. Zatem energia kinetyczna zależy od wyboru układu odniesienia.

Energia potencjalna- energia mechaniczna układu ciał, określona przez ich względne położenie i charakter sił wzajemnego oddziaływania między nimi.

Kiedy ciała oddziałują poprzez pola sił (pola sił sprężystych, grawitacyjnych), praca wykonana przez działające siły podczas poruszania się ciała nie zależy od trajektorii tego ruchu, lecz zależy jedynie od początkowego i końcowego położenia ciała. Takie pola nazywane są potencjał, a działające w nich siły są konserwatywny. Jeżeli praca wykonana przez siłę zależy od toru ruchu ciała z jednego punktu do drugiego, wówczas taką siłę nazywamy rozpraszający(siła tarcia). Ciało znajdujące się w potencjalnym polu sił ma energię potencjalną P. Praca sił zachowawczych przy elementarnej (nieskończenie małej) zmianie konfiguracji układu jest równa przyrostowi energii potencjalnej przyjętej ze znakiem minus: dA = - dP (6)

Praca D A- iloczyn skalarny siły F i przemieszczenia dr oraz wyrażenia (6) można zapisać: Fdr= -dП (7)

Podczas obliczeń energię potencjalną ciała w określonym położeniu uważa się za równą zeru (wybiera się zerowy poziom odniesienia), a energię ciała w innych położeniach mierzy się w stosunku do poziom zerowy.

Konkretna postać funkcji P zależy od charakteru pola siłowego. Na przykład energia potencjalna ciała o masie T, podniesiony do wysokości H nad powierzchnią Ziemi jest równa (8)

gdzie jest wysokość H liczony jest od poziomu zerowego, dla którego P 0 = 0.

Ponieważ początek jest wybierany arbitralnie, energia potencjalna może mieć wartość ujemną (energia kinetyczna jest zawsze dodatnia!). Jeżeli energię potencjalną ciała leżącego na powierzchni Ziemi przyjmiemy za zero, to energia potencjalna ciała znajdującego się na dnie kopalni (głębokość H" ), P= - mgh".

Energia potencjalna układu jest funkcją stanu układu. Zależy to jedynie od konfiguracji systemu i jego położenia względem ciał zewnętrznych.

Całkowita energia mechaniczna układu równa sumie energii kinetycznej i potencjalnej: E=T+P.

1,5. PRACA MECHANICZNA I ENERGIA KINETYCZNA

Pojęcie energii. Energia mechaniczna. Praca jest ilościową miarą zmiany energii. Praca sił wypadkowych. Praca sił w mechanice. Pojęcie władzy. Energia kinetyczna jako miara ruchu mechanicznego. Zmiana komunikacji ki energia netto z pracą sił wewnętrznych i zewnętrznych.Energia kinetyczna układu w różnych układach odniesienia.Twierdzenie Koeniga.

Energia - jest uniwersalną miarą różnych form ruchu i interakcji. M energia mechaniczna opisuje kwotę potencjałIenergia kinetyczna, dostępne w komponentach układ mechaniczny . Energia mechaniczna- jest to energia związana z ruchem obiektu lub jego położeniem, zdolność do wykonywania pracy mechanicznej.

Praca siły - jest to ilościowa charakterystyka procesu wymiany energii pomiędzy oddziałującymi ciałami.

Niech cząstka pod wpływem siły porusza się po określonej trajektorii 1-2 (ryc. 5.1). Ogólnie rzecz biorąc, siła w procesie

Ruch cząstki może zmieniać się zarówno pod względem wielkości, jak i kierunku. Rozważmy, jak pokazano na ryc. 5.1, elementarne przemieszczenie, w obrębie którego siłę można uznać za stałą.

Wpływ siły na przemieszczenie charakteryzuje się wartością równą iloczynowi skalarnemu, który nazywa się podstawowa praca poruszające się siły. Można to przedstawić w innej formie:

,

gdzie jest kątem między wektorami i jest ścieżką elementarną, wskazany jest rzut wektora na wektor (ryc. 5.1).

A więc elementarna praca siły na przemieszczenie

Wielkość ma charakter algebraiczny: w zależności od kąta między wektorami siły i/lub od znaku rzutu wektora siły na wektor przemieszczenia może być dodatnia lub ujemna, a w szczególności równa zero, jeśli tj. . Jednostką pracy w układzie SI jest dżul, w skrócie J.

Sumując (całkując) wyrażenie (5.1) po wszystkich elementarnych odcinkach ścieżki od punktu 1 do punktu 2, znajdujemy pracę wykonaną przez siłę przy danym przemieszczeniu:

jasne jest, że praca elementarna A jest liczbowo równa powierzchni zacieniowanego paska, a praca A na ścieżce od punktu 1 do punktu 2 jest obszarem figury ograniczonym krzywą, rzędnymi 1 i 2 i oś s. W tym przypadku obszar figury nad osią s jest brany ze znakiem plus (odpowiada to pracy dodatniej), a obszar figury pod osią s ze znakiem minus ( odpowiada to pracy negatywnej).

Spójrzmy na przykłady obliczania pracy. Praca siły sprężystej gdzie jest wektorem promienia cząstki A względem punktu O (rys. 5.3).

Przesuńmy cząstkę A, na którą działa ta siła, po dowolnej drodze z punktu 1 do punktu 2. Najpierw znajdźmy elementarną pracę siły na elementarne przemieszczenie:

.

Produkt skalarny gdzie jest rzutem wektora przemieszczenia na wektor . Ten rzut jest równy przyrostowi modułu wektora.

Obliczmy teraz pracę wykonaną przez tę siłę na całej drodze, czyli całkujmy ostatnie wyrażenie od punktu 1 do punktu 2:

Obliczmy pracę wykonaną przez siłę grawitacji (lub matematycznie analogiczną siłę Coulomba). Niech na początku wektora znajduje się nieruchoma masa punktowa (ładunek punktowy) (ryc. 5.3). Wyznaczmy pracę wykonaną przez siłę grawitacji (Coulomba), gdy cząstka A przemieszcza się z punktu 1 do punktu 2 po dowolnej drodze. Siłę działającą na cząstkę A można przedstawić w następujący sposób:

gdzie parametr dla oddziaływania grawitacyjnego jest równy , a dla oddziaływania Coulomba jego wartość jest równa . Obliczmy najpierw elementarną pracę tej siły przy przemieszczeniu

Podobnie jak w poprzednim przypadku, iloczyn skalarny jest zatem

.

Praca tej siły od punktu 1 do punktu 2

Rozważmy teraz działanie jednorodnej siły ciężkości. Zapiszmy tę siłę w postaci, w której wskazana jest jednostka jednostkowa osi pionowej z o kierunku dodatnim (ryc. 5.4). Elementarna praca grawitacji na przemieszczenie

Produkt skalarny gdzie rzut na jednostkę jednostkową jest równy przyrostowi współrzędnej z. Dlatego wyrażenie pracy przyjmuje formę

Praca wykonana przez daną siłę na całej drodze od punktu 1 do punktu 2

Rozpatrywane siły są interesujące w tym sensie, że ich praca, jak wynika ze wzorów (5.3) - (5.5), nie zależy od kształtu toru pomiędzy punktami 1 i 2, lecz zależy jedynie od położenia tych punktów . Ta bardzo ważna cecha tych sił nie jest jednak nieodłączna dla wszystkich sił. Na przykład siła tarcia nie ma tej właściwości: praca tej siły zależy nie tylko od położenia punktów początkowych i końcowych, ale także od kształtu ścieżki między nimi.

Do tej pory mówiliśmy o działaniu jednej siły. Jeżeli w procesie ruchu na cząstkę działa kilka sił, których wypadkowa jest wówczas łatwo wykazać, że praca powstałej siły przy pewnym przemieszczeniu jest równa sumie algebraicznej pracy wykonanej przez każdą z sił oddzielnie na tym samym przemieszczeniu. Naprawdę,

Wprowadźmy do rozważań nową wielkość – moc. Służy do scharakteryzowania szybkości wykonywania pracy. Moc , a-przeor, - jest pracą wykonaną przez siłę w jednostce czasu . Jeśli siła działa przez pewien okres czasu, wówczas moc rozwinięta przez tę siłę w danym momencie wynosi. Biorąc to pod uwagę, otrzymujemy

Jednostką mocy w układzie SI jest wat, w skrócie W.

Zatem moc wytworzona przez siłę jest równa iloczynowi skalarnemu wektora siły i wektora prędkości, z jaką porusza się punkt przyłożenia tej siły. Podobnie jak praca, moc jest wielkością algebraiczną.

Znając moc tej siły, możesz obliczyć pracę wykonaną przez tę siłę w czasie t. Rzeczywiście, przedstawiając całkę w (5.2) jako dostajemy

Warto zwrócić także uwagę na jedną bardzo istotną okoliczność. Mówiąc o pracy (lub władzy) należy w każdym konkretnym przypadku jasno wskazać lub wyobrazić sobie pracę jaka siła(lub siły). W przeciwnym razie z reguły nieporozumienia są nieuniknione.

Rozważmy koncepcję energia kinetyczna cząstek. Niech cząstka masy T porusza się pod wpływem jakiejś siły (w ogólnym przypadku siła ta może być wypadkową kilku sił). Znajdźmy elementarną pracę, jaką ta siła wykonuje przy elementarnym przemieszczeniu. Mając to na uwadze i , piszemy

.

Produkt skalarny gdzie jest rzutem wektora na kierunek wektora. Rzut ten jest równy przyrostowi wielkości wektora prędkości. Dlatego elementarna praca

Z tego jasno wynika, że ​​praca powstałej siły zwiększa pewną wartość w nawiasach, która nazywa się energia kinetyczna cząsteczki.

oraz po ostatecznym przesunięciu z punktu 1 do punktu 2

tj. przyrost energii kinetycznej cząstki przy pewnym przemieszczeniu jest równy algebraicznej sumie pracy wszystkich sił, działając na cząstkę przy tym samym przemieszczeniu. Jeżeli wtedy energia kinetyczna cząstki wzrośnie; jeśli tak jest, to energia kinetyczna maleje.

Równanie (5.9) można przedstawić w innej formie, dzieląc obie strony przez odpowiedni przedział czasu dt:

Oznacza to, że pochodna energii kinetycznej cząstki po czasie jest równa mocy N wypadkowej siły działającej na cząstkę.

Teraz przedstawmy tę koncepcję energia kinetyczna układu . Rozważmy dowolny układ cząstek w pewnym układzie odniesienia. Niech cząstka układu ma w danym momencie energię kinetyczną. Przyrost energii kinetycznej każdej cząstki jest równy, zgodnie z (5.9), pracy wszystkich sił działających na tę cząstkę: Znajdźmy elementarną pracę wykonaną przez wszystkie siły działające na wszystkie cząstki układu:

gdzie jest całkowitą energią kinetyczną układu. Należy pamiętać, że energia kinetyczna układu jest wielkością przyłączeniowy : jest równa sumie energii kinetycznych poszczególnych części układu, niezależnie od tego, czy oddziałują one ze sobą, czy nie.

Więc, przyrost energii kinetycznej układu jest równy pracy wykonanej przez wszystkie siły działające na wszystkie cząstki układu. Z elementarnym ruchem wszystkich cząstek

i w ostatnim ruchu

tj. pochodna czasowa energii kinetycznej układu jest równa sumie mocy wszystkich sił działających na wszystkie cząstki układu,

Twierdzenie Koeniga: energia kinetyczna K układy cząstek można przedstawić jako sumę dwóch składników: a) energii kinetycznej mV C 2 /2 wyimaginowany punkt materialny, którego masa jest równa masie całego układu i którego prędkość pokrywa się z prędkością środka masy; b) energia kinetyczna K wzgl układ cząstek obliczony w układzie środka masy.